
【题目】冠状病毒是一个大型病毒家族,已知可引起感冒以及中东呼吸综合征(MERS)和严重急性呼吸综合征(SARS)等较严重疾病.而今年出现的新型冠状病毒(nCoV)是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中,感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.应国务院要求,黑龙江某医院选派医生参加援鄂医疗,该院呼吸内科有3名男医生,2名女医生,其中李亮(男)为科室主任;该院病毒感染科有2名男医生,2名女医生,其中张雅(女)为科室主任,现在院方决定从两科室中共选4人参加援鄂医疗(最后结果用数字表达).
(1)若至多有1名主任参加,有多少种派法?
(2)若呼吸内科至少2名医生参加,有多少种派法?
(3)若至少有1名主任参加,且有女医生参加,有多少种派法?
【答案】(1)105种(2)105种(3)87种.
【解析】
(1)至多有1名主任参加,包括两种情况:一种是无主任参加,另一种是只有1名主任参加,利用分类计数原理可得结果;
(2)呼吸内科至少2名医生参加,分三种情况:第一种是呼吸内科2名医生参加,第二种呼吸内科3名医生参加,第三种呼吸内科4名医生参加,然后利用分类计数原理可得结果;
(3)由于张雅既是主任,也是女医生.属于特殊元素,优先考虑,分有张雅和无张雅两种情况求解即可.
(1)直接法:若无主任![]() ,若只有1名主任
,若只有1名主任![]() ,共105种,
,共105种,
间接法:![]() .
.
(2)直接法:![]() ,
,
间接法:![]() .
.
(3)张雅既是主任,也是女医生.属于特殊元素,优先考虑,所以以是否有张雅来分类.
第一类:若有张雅![]() ,
,
第二类:若无张雅,则李亮必定去![]() ,共87种.
,共87种.


科目:高中数学 来源: 题型:
【题目】已知![]() 的三边长为a,b,c,有下列四个命题:
的三边长为a,b,c,有下列四个命题:
①以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在;
为边长的三角形一定存在;
②以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在;
为边长的三角形一定存在;
③以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在;
为边长的三角形一定存在;
④以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在.
为边长的三角形一定存在.
其中正确的是( )
A.①③B.②③C.②④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,(其中
,(其中![]() 为自然对数的底数,
为自然对数的底数,![]() …).
…).
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)若函数![]() 在区间
在区间![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(3)若![]() ,当
,当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周上有800个点,依顺时针方向标号为![]() ,它们将圆周分成800个间隙.今选定某一点染成红色,然后按如下规则,逐次染红其余的一些点:如果第
,它们将圆周分成800个间隙.今选定某一点染成红色,然后按如下规则,逐次染红其余的一些点:如果第![]() 号点已被染红,则可按顺时针方向转过
号点已被染红,则可按顺时针方向转过![]() 个间隙,再将所到达的那个端点染红.如此继续下去.试问圆周上最多可得到多少个红点?证明你的结论.
个间隙,再将所到达的那个端点染红.如此继续下去.试问圆周上最多可得到多少个红点?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品.现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
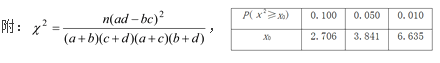
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定两个七棱锥,它们有公共面的底面![]() ,顶点
,顶点![]() 、
、![]() 在底面的两则.现将下述线段中的每一条染红、蓝两色之一:
在底面的两则.现将下述线段中的每一条染红、蓝两色之一:![]() ,底面上的所有对角线和所有的侧棱.求证:图中心存在一个同色三角形.
,底面上的所有对角线和所有的侧棱.求证:图中心存在一个同色三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Sn为数列{an}的前n项和,且Sn+2=2an,n∈N*.
(1)求数列{an}的通项公式;
(2)令bn![]() ,设数列{bn}的前项和为Tn,若Tn
,设数列{bn}的前项和为Tn,若Tn![]() ,求n的最小值.
,求n的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com