
【题目】2013年至201 9年我国二氧化硫的年排放量(单位:万吨)如下表,则以下结论中错误的是( )
![]()
A.二氧化硫排放量逐年下降
B.2018年二氧化硫减排效果最为显著
C.2017年至2018年二氧化硫减排量比2013年至2016年二氧化硫减排量的总和大
D.2019年二氧化硫减排量比2018年二氧化硫减排量有所增加
【答案】D
【解析】
采用逐一验证法,根据数据的简单分析,可得结果.
A正确
根据数据可知,二氧化硫排放量逐年下降
B正确
从2017年到2018年,下降了756.24万吨,
是所有相邻年份二氧化硫减排量最大的,
所以2018年二氧化硫减排效果最为显著
C正确
2017年至2018年二氧化硫减排量为756.24万吨
2013年至2016年二氧化硫减排量的总和为2217.9-1974.4=243.5万吨
所以243.5<756.24,故C正确
D错
2017年至2018年二氧化硫减排量为756.24万吨
2018年至2019年二氧化硫减排量为1102.86-1014.6=88.26万吨
故2019年二氧化硫减排量比2018年二氧化硫减排量有所减少.
故选:D.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数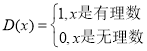 ,被称为狄利克雷函数.以下说法正确的是( ).
,被称为狄利克雷函数.以下说法正确的是( ).
A.![]() 的值域是
的值域是![]()
B.![]() ,都有
,都有![]()
C.存在非零实数![]() ,使得
,使得![]()
D.对任意![]() ,都有
,都有![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
平面直角坐标系xOy中,曲线C:![]() .直线l经过点P(m,0),且倾斜角为
.直线l经过点P(m,0),且倾斜角为![]() .O为极点,以x轴正半轴为极轴,建立极坐标系.
.O为极点,以x轴正半轴为极轴,建立极坐标系.
(Ⅰ)写出曲线C的极坐标方程与直线l的参数方程;
(Ⅱ)若直线l与曲线C相交于A,B两点,且|PA|·|PB|=1,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为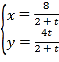 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() (
(![]() )与直线
)与直线![]() 和曲线
和曲线![]() 分别交于
分别交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房地产开发商有一块如图(1)所示的四边形空地ABCD,经测量,边界CB与CD的长都为2km,所形成的角∠![]() .
.
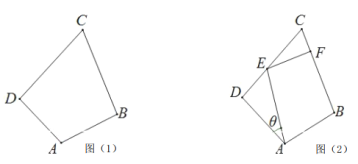
(I)如果边界AD与AB所形成的角![]() ,现欲将该地块用固定高度的板材围成一个封闭的施工场地,求至多购买多少千米长度的板材;
,现欲将该地块用固定高度的板材围成一个封闭的施工场地,求至多购买多少千米长度的板材;
(II)当边界AD与CD垂直,AB与BC垂直时,为后期开发方便,拟在这块空地上先建两条内部道路AE,EF,如图(2)所示,点E在边界CD上,且道路EF与边界BC互相垂直,垂足为F,为节约成本,欲将道路AE,EF分别建成水泥路、砂石路,每1km的建设费用分别为![]() 、a元(a为常数);若设
、a元(a为常数);若设![]() ,试用
,试用![]() 表示道路AE,EF建设的总费用
表示道路AE,EF建设的总费用![]() (单位:元),并求出总费用
(单位:元),并求出总费用![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系;曲线C1的普通方程为(x-1)2 +y2 =1,曲线C2的参数方程为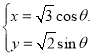 (θ为参数).
(θ为参数).
(Ⅰ)求曲线C1和C2的极坐标方程:
(Ⅱ)设射线θ=![]() (ρ>0)分别与曲线C1和C2相交于A,B两点,求|AB|的值.
(ρ>0)分别与曲线C1和C2相交于A,B两点,求|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,PA=AB=1,![]()

(1)证明:BD⊥平面PAC;
(2)若E是PC的中点,F是棱PD上一点,且BE∥平面ACF,求二面角F﹣AC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,点
,点![]() 是椭圆
是椭圆![]() 上一点,以
上一点,以![]() 为直径的圆
为直径的圆![]() :
: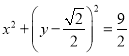 过点
过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且斜率大于0的直线
且斜率大于0的直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,过点
,过点![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与直线
与直线![]() 交于点
交于点![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com