练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知|
    a
    |=1，|
    b
    |=2，＜
    a
    ，
    b
    ＞=60°    ，则|2
    a
    -
    b
    |    =（　　）
    A．2B．4C．2
    		2
    		D．8
    ∵|
    a
    |=1，|
    b
    |=2，＜
    a
    ，
    b
    ＞=60°    ，
    ∴
    a
    •
    b
    =|
    a
    |•|
    b
    |•cos60°    =1×2×
    1
    2
    =1，
    因此(2
    a
    -
    b
    )2    =4|
    a
    |2-4
    a
    •
    b
    +|
    b
    |2=4×12-4×1+22=4，
    ∴|2
    a
    -
    b
    |    =
    		(2
    a
    -
    b
    )    2
    =2（舍负）．
    故选：A
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

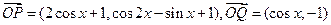
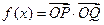
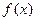
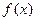
    （本小题满分12分）已知向量,定义（1）求函数的单调递减区间；（2）求函数的最大值及取得最大值时的x的取值集合。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知
    a
    、
    b
    均为单位向量，且|
    a
    +2
    b
    |=
    		7
    ，那么向量
    a
    与
    b
    的夹角为（　　）
    A．
    π
    6
    		B．
    π
    3
    		C．
    5π
    6
    		D．
    2π
    3

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知|
    a
    |=|
    b
    |=2，（
    a
    +2
    b
    ）•（
    a
    -
    b
    ）=-2，则
    a
    与
    b
    的夹角为______．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知在△ABC中，∠A=120°，记
    α
    =
    BA
    |
    BA
    |cosA
    +
    BC
    |
    BC
    |cosC
    ，
    β
    =
    CA
    |CA|
    cosA
    +
    CB
    |
    CB
    |sinB
    CB
    |
    CB
    |cosB
    ，则向量
    α
    与
    β
    的夹角为______．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

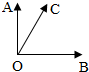
    如图所示：|
    OA
    |=2，
    OB
    =2
    		3
    ，且
    OA
    •
    OB
    =0，∠AOC=
    π
    6
    ，设
    OC
    =λ
    OA
    +μ
    OB
    ，则
    λ
    μ
    =（　　）
    A．
    		3
    3
    		B．
    1
    3
    		C．3D．
    		3

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知向量
    m
    =（λ+1，1），
    n
    =（λ+2，2），若（
    m
    +
    n
    ）⊥（
    m
    -
    n
    ），λ=______．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知抛物线C1：x2=8y和圆C2：x2+（y-2）2=4，直线l过C1焦点，且与C1，C2交于四点，从左到右依次为A，B，C，D，则
    AB
    •
    CD
    =______．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

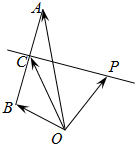
    如图，O，A，B是平面上的三点，向量
    OA
    =
    a
    ，
    OB
    =
    b
    设P为线段AB的垂直平分线CP上任意一点，向量
    OP
    =
    P
    ，若|
    .
    a
    |=4，|
    .
    b
    |=2，则
    p
    •（
    a
    -
    b
    ）=（　　）
    A．1B．3C．5D．6

    查看答案和解析>>

    同步练习册答案