
【题目】函数f(x)=x2+acosx+bx,非空数集A={x|f(x)=0},B={x|f(f(x))=0},已知A=B,则参数a的所有取值构成的集合为_____;参数b的所有取值构成的集合为_____.
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】如图,已知点F为抛物线C:![]() (
(![]() )的焦点,过点F的动直线l与抛物线C交于M,N两点,且当直线l的倾斜角为45°时,
)的焦点,过点F的动直线l与抛物线C交于M,N两点,且当直线l的倾斜角为45°时,![]() .
.
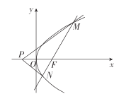
(1)求抛物线C的方程.
(2)试确定在x轴上是否存在点P,使得直线PM,PN关于x轴对称?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司新发明了甲、乙两种不同型号的手机,公司统计了消费者对这两种型号手机的评分情况,作出如下的雷达图,则下列说法不正确的是( )

A. 甲型号手机在外观方面比较好.B. 甲、乙两型号的系统评分相同.
C. 甲型号手机在性能方面比较好.D. 乙型号手机在拍照方面比较好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,下列命题:
,下列命题:
①![]() 的定义域为
的定义域为![]() ;
;
②![]() 是奇函数;
是奇函数;
③![]() 在
在![]() 上单调递增;
上单调递增;
④若实数![]() 满足
满足![]() ,则
,则![]() ;
;
⑤设函数![]() 在上的最大值为
在上的最大值为![]() ,最小值为
,最小值为![]() ,则
,则![]() .
.
其中真命题的序号是______.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosxsin(x+2φ)为偶函数,其中φ∈(0,![]() ),则下列关于函数g(x)=sin(2x+φ)的描述正确的是( )
),则下列关于函数g(x)=sin(2x+φ)的描述正确的是( )
A.g(x)在区间[![]() ]上的最小值为﹣1
]上的最小值为﹣1
B.g(x)的图象可由函数f(x)的图象向上平移一个单位,再向右平移![]() 个单位长度得到
个单位长度得到
C.g(x)的图象的一个对称中心为(![]() ,0)
,0)
D.g(x)的一个单调递增区间为[0,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com