
【题目】如图,在四面体![]() 中,
中,![]() 分别为
分别为![]() 的中点,过
的中点,过![]() 任作一个平面
任作一个平面![]() 分别与直线
分别与直线![]() 相交于点
相交于点![]() ,则下列结论正确的是___________.①对于任意的平面
,则下列结论正确的是___________.①对于任意的平面![]() ,都有直线
,都有直线![]() ,
,![]() ,
,![]() 相交于同一点;②存在一个平面
相交于同一点;②存在一个平面![]() ,使得点
,使得点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 的延长线上; ③对于任意的平面
的延长线上; ③对于任意的平面![]() ,都有
,都有![]() ;④对于任意的平面
;④对于任意的平面![]() ,当
,当![]() 在线段
在线段![]() 上时,几何体
上时,几何体![]() 的体积是一个定值.
的体积是一个定值.

【答案】③④
【解析】
当![]() 分别为
分别为![]() 中点时,可知三线互相平行,排除①;若三线相交,交点必在
中点时,可知三线互相平行,排除①;若三线相交,交点必在![]() 上,可排除②;取
上,可排除②;取![]() 中点
中点![]() ,利用线面平行判定定理可证得
,利用线面平行判定定理可证得![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,再结合
,再结合![]() 为
为![]() 中点可得
中点可得![]() 到平面
到平面![]() 的距离相等,进一步得到
的距离相等,进一步得到![]() 到直线
到直线![]() 的距离相等,从而证得面积相等,③正确;首先通过临界状态
的距离相等,从而证得面积相等,③正确;首先通过临界状态![]() 与
与![]() 重合,
重合,![]() 与
与![]() 重合时,求得所求体积为四面体体积一半;当不位于临界状态时,根据③的结论可证得
重合时,求得所求体积为四面体体积一半;当不位于临界状态时,根据③的结论可证得![]() ,从而可知所求体积为四面体体积一半,进而可知为定值,④正确.
,从而可知所求体积为四面体体积一半,进而可知为定值,④正确.
当![]() 分别为
分别为![]() 中点时,
中点时,![]() ,则①错误
,则①错误
若![]() 三线相交,则交点
三线相交,则交点![]()
![]() 不存在
不存在![]() 在线段
在线段![]() 上,
上,![]() 在线段
在线段![]() 延长线上的情况,则②错误
延长线上的情况,则②错误
取![]() 中点
中点![]() ,如图
,如图![]() 所示:
所示:
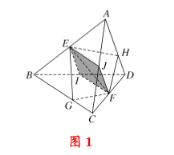
![]() 分别为
分别为![]() 中点
中点 ![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
同理可得:![]() 平面
平面![]()
![]() 到平面
到平面![]() 的距离相等;
的距离相等;![]() 到平面
到平面![]() 的距离相等
的距离相等
又![]() 为
为![]() 中点
中点 ![]() 到平面
到平面![]() 的距离相等
的距离相等
![]() 到平面
到平面![]() 的距离相等
的距离相等
连接![]() 交
交![]() 于
于![]() ,则
,则![]() 为
为![]() 中点
中点 ![]() 到
到![]() 距离相等
距离相等
![]() ,则③正确
,则③正确
当![]() 与
与![]() 重合,
重合,![]() 与
与![]() 重合时,此时几何体体积为三棱锥
重合时,此时几何体体积为三棱锥![]() 的体积
的体积
![]() 为
为![]() 中点
中点 ![]() 三棱锥
三棱锥![]() 的体积为四面体
的体积为四面体![]() 体积的一半
体积的一半

当如图![]() 所示时,由③可知
所示时,由③可知![]()
又![]() 为
为![]() 中点
中点 ![]() 到截面的距离相等
到截面的距离相等 ![]()
![]()
![]()
综上所述,几何体![]() 的体积为四面体
的体积为四面体![]() 体积的一半,为定值,则④正确
体积的一半,为定值,则④正确
本题正确结果:③④


科目:高中数学 来源: 题型:
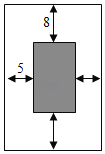
【题目】淄博七中、临淄中学为了加强交流,增进友谊,两校准备举行一场足球赛,由淄博七中版画社的同学设计一幅矩形宣传画,要求画面面积为![]() ,画面的上、下各留
,画面的上、下各留![]() 空白,左、右各留
空白,左、右各留![]() 空白.如何设计画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?
空白.如何设计画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一种游戏画板,要求参与者用六种颜色给画板涂色,这六种颜色分别为红色、黄色1、黄色2、黄色3、金色1、金色2,其中黄色1、黄色2、黄色3是三种不同的颜色,金色1、金色2是两种不同的颜色,要求红色不在两端,黄色1、黄色2、黄色3有且仅有两种相邻,则不同的涂色方案有( )

A.120种B.240种C.144种D.288种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某热带风暴中心B位于海港城市A东偏南30°的方向,与A市相距400km.该热带风暴中心B以![]() 的速度向正北方向移动,影响范围的半径是350km.问:从此时起,经多长时间后A市将受热带风暴影响,大约受影响多长时间?
的速度向正北方向移动,影响范围的半径是350km.问:从此时起,经多长时间后A市将受热带风暴影响,大约受影响多长时间?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为边长为2的菱形,
为边长为2的菱形,![]() ,
,![]() ,面
,面![]() 面
面![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.

(1)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 面
面![]() ,并说明理由;
,并说明理由;
(2)当二面角![]() 的余弦值为
的余弦值为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种汽车的元件,该元件是经过![]() 、
、![]() 、
、![]() 三道工序加工而成的,
三道工序加工而成的,![]() 、
、![]() 、
、![]() 三道工序加工的元件合格率分别为
三道工序加工的元件合格率分别为![]() 、
、![]() 、
、![]() .已知每道工序的加工都相互独立,三道工序加工都合格的元件为一等品;恰有两道工序加工合格的元件为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工都合格的元件为一等品;恰有两道工序加工合格的元件为二等品;其它的为废品,不进入市场.
(Ⅰ)生产一个元件,求该元件为二等品的概率;
(Ⅱ)若从该工厂生产的这种元件中任意取出3个元件进行检测,求至少有2个元件是一等品的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com