
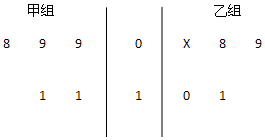
 如图茎叶图记录了甲乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示
如图茎叶图记录了甲乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示分析 (1)x=8时,能求出乙组同学植树棵树的平均数与方差.
(2)记甲组四名同学为A1、A2、A3、A4,他们植树棵数依次为9、9、11、11;乙组四名同学为B1、B2、B3、B4,他们植树棵数依次为9、8、9、10.利用列举法能求出x=9时,这两名同学植树总棵数为19的概率.
解答 解:(1)x=8时,平均数$\overline{x}$=$\frac{8+8+9+10}{4}$=8.75,…(2分)
方差S2=$\frac{1}{4}$[(8-8.75)2+(8-8.75)2+(9-8.75)2+(10-8.75)2]=0.6875.…(5分)
(2)记甲组四名同学为A1、A2、A3、A4,
他们植树棵数依次为9、9、11、11;
乙组四名同学为B1、B2、B3、B4,
他们植树棵数依次为9、8、9、10.
∴基本事件有:
(A1,B1),(A1,B2),(A1,B3),(A1,B4),(A2,B1),(A2,B2),
(A2,B3),(A2,B4),(A3,B1),(A3,B2),(A3,B3),(A3,B4),
(A4,B1),(A4,B2),(A4,B3),(A4,B4)共16个. …(9分)
设选出两名同学的植树总棵数为19的事件为C,则C有4个结果,
它们是(A1,B4),(A2,B4),(A3,B2),(A4,B2),…(11分)
∴x=9时,这两名同学植树总棵数为19的概率P(C)=$\frac{4}{16}=\frac{1}{4}$.…(12分)
点评 本题考查茎叶图的应用,查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
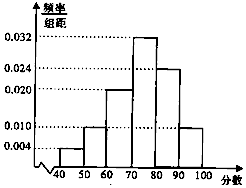 某校从高二年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
某校从高二年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | (-2,-1] | C. | (-2,0] | D. | (-∞,0] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com