Question

【题目】在四棱锥P﹣ABCD中，底面ABCD是边长为2的菱形，∠BAD=60°，PD⊥底面ABCD，点M、N分别是棱AB、CD的中点．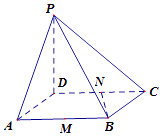
（1）证明：BN⊥平面PCD；
（2）在线段PC上是否存在点H，使得MH与平面PCD所成最大角的正切值为 ，若存在，请求出H点的位置；若不存在，请说明理由．

Answer 1

【答案】
（1）证明：连接BD，

∵四边形ABCD为菱形，∠BCD=∠BAD=60°

∴△BCD为正三角形，∵N为CD中点，所以BN⊥CD

∵PD⊥平面ABCD，BN平面ABCD，∴PD⊥BN，

又PD平面PCD，CD平面PCD，CD∩PD=D，∴BN⊥平面PCD

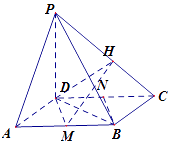
（2）解：假设线段PC上存在一点H，连接MH，DH，MD，

MBDN为平行四边形，∴MD∥BN，

由（1）BN⊥平面PCD∴MD⊥平面PCD，∴∠MHD为MH与平面PCD所成的角

在直角三角形MDH中， ，当DH最小，即DH⊥PC时，∠DHM最大，

，

∴

在Rt△DHC中 ，∴

∴线段PC上存在点H，当 时，使MH与平面PCD所成最大角的正切值为

【解析】（1）连接BD，证明：BN⊥CD，PD⊥BN，即可证明BN⊥平面PCD；（2）假设线段PC上存在一点H，连接MH，DH，MD，可得∠MHD为MH与平面PCD所成的角，在直角三角形MDH中， ，当DH最小，即DH⊥PC时，∠DHM最大，利用条件求出CH，即可得出结论．