
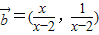 ,
,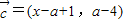 ,解关于x的不等式
,解关于x的不等式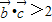 (其中a>1)
(其中a>1)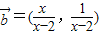 ,
,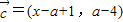 ,根据平面向量的数量积公式,我们易求出
,根据平面向量的数量积公式,我们易求出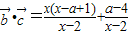 ,进而可将不等式
,进而可将不等式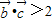 转化为(x-a)(x-1)(x-2)>0,由a>1,我们分1<a<2,a=2和a>2三种情况分别求出不等式的解集,即可得到答案.
转化为(x-a)(x-1)(x-2)>0,由a>1,我们分1<a<2,a=2和a>2三种情况分别求出不等式的解集,即可得到答案.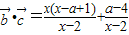 ,(2分)
,(2分)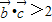 ,得
,得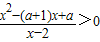
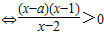 (4分)
(4分)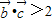 转化为(x-a)(x-1)(x-2)>0是解答本题的关键.
转化为(x-a)(x-1)(x-2)>0是解答本题的关键. 

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com