[题目]为了解数学课外兴趣小组的学习情况,从某次测试的成绩中随机抽取名学生的成绩进行分析,得到如图所示的频率分布直方图.(1)根据频率分布直方图估计本次测试成绩的众数;(2)从成绩不低于分的两组学生中任选人,求选出的两人来自同一组的概率. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】为了解数学课外兴趣小组的学习情况,从某次测试的成绩中随机抽取名学生的成绩进行分析,得到如图所示的频率分布直方图.

（1）根据频率分布直方图估计本次测试成绩的众数;

（2）从成绩不低于分的两组学生中任选人,求选出的两人来自同一组的概率.

【答案】（1）（2）

【解析】

（1）根据频率分布直方图,即可求得答案;

（2）根据已知条件可得在抽取的名学生中,成绩在区间的人数为:,这人分别记为成绩在区间的人数为:,这人分别记为,若从成绩不低于分的两组学生中任选人,写出基本事件空间,即可求得答案.

（1）根据频率分布直方图可估计本次测试成绩的众数为:

（2）根据已知条件可得在抽取的名学生中,

成绩在区间的人数为:,这人分别记为

若从成绩不低于分的两组学生中任选人,

其所有情况有:共个基本事件,

其中两人来自同一组所含基本事件有:共个.

选出的两人来自同一组的概率为:

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数.

（1）若，讨论的单调性；

（2）若，且对于函数的图象上两点，，存在，使得函数的图象在处的切线.求证；.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】十九大以来，某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求，带领广大农村地区人民群众脱贫奔小康.经过不懈的奋力拼搏，新农村建设取得巨大进步，农民年收入也逐年增加.为了制定提升农民年收入、实现2020年脱贫的工作计划，该地扶贫办统计了2019年50位农民的年收入并制成如下频率分布直方图：

（1）根据频率分布直方图，估计50位农民的年平均收入元（单位：千元）（同一组数据用该组数据区间的中点值表示）；

（2）由频率分布直方图，可以认为该贫困地区农民年收入X服从正态分布，其中近似为年平均收入，近似为样本方差，经计算得，利用该正态分布，求：

（i）在扶贫攻坚工作中，若使该地区约有占总农民人数的84.14%的农民的年收入高于扶贫办制定的最低年收入标准，则最低年收入大约为多少千元？

（ii）为了调研“精准扶贫，不落一人”的政策要求落实情况，扶贫办随机走访了1000位农民.若每位农民的年收入互相独立，问：这1000位农民中的年收入不少于12.14千元的人数最有可能是多少？

附参考数据：，若随机变量X服从正态分布，则，，.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）＝ex－ax－1（e为自然对数的底数），a＞0．

（1）若函数f（x）恰有一个零点，证明：aa＝ea－1；

（2）若f（x）≥0对任意x∈R恒成立，求实数a的取值集合．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，圆柱的轴截面是边长为2的正方形，点是圆弧上的一动点（不与重合），点是圆弧的中点，且点在平面的两侧.

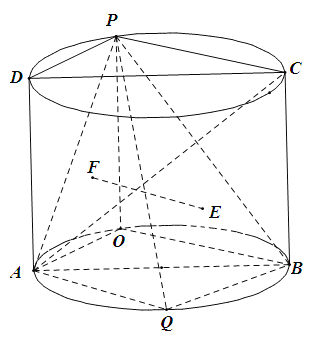
（1）证明：平面平面；

（2）设点在平面上的射影为点，点分别是和的重心，当三棱锥体积最大时，回答下列问题.

（ⅰ）证明：平面；

（ⅱ）求平面与平面所成二面角的正弦值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，已知四边形ABCD是正方形，AE⊥平面ABCD，PD∥AE，PD＝AD＝2EA＝2，G，F，H分别为BE，BP，PC的中点．

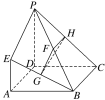
（1）求证：平面ABE⊥平面GHF；

（2）求直线GH与平面PBC所成的角θ的正弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知在椭圆上，为右焦点，轴，为椭圆上的四个动点，且，交于原点.

（1）判断直线与椭圆的位置关系；

（2设，满足，判断的值是否为定值，若是，请求出此定值，并求出四边形面积的最大值，否则说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】“二万五千里长征”是1934年10月到1936年10月中国工农红军进行的一次战略转移，是人类历史上的伟大奇迹，向世界展示了中国工农红军的坚强意志，在期间发生了许多可歌可泣的英雄故事.在中国共产党建党周年之际，某中学组织了“长征英雄事迹我来讲”活动，已知该中学共有高中生名，用分层抽样的方法从该校高中学生中抽取一个容量为的样本参加活动，其中高三年级抽了人，高二年级抽了人，则该校高一年级学生人数为（）