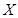练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    甲班有2名男乒乓球选手和3名女乒乓球选手，乙班有3名男乒乓球选手和1名女乒乓球选手，学校计划从甲乙两班各选2名选手参加体育交流活动.
    （Ⅰ）求选出的4名选手均为男选手的概率.
    （Ⅱ）记为选出的4名选手中女选手的人数，求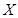的分布列和期望.
    （Ⅰ）
    （Ⅱ）的分布列为










    期望为
    (I)选出的4名选手均为男选手有种选法.总的结果有，所以所求事件的概率为.事件表示“选出的4名选手均为男选手”.由题意知
     .
    (II)先确定的可能取值为，然后求出每个值对应的概率，再列出分布列，利用期望公式求期望即可.的可能取值为. ，    ，   ，
    .      
    的分布列：










    .
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    (本小题满分12分)
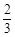    已知一种名贵花卉种子的发芽率为，现种植这种种子4粒，求：
    （Ⅰ）至少有3粒发芽的概率；
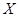    （Ⅱ）种子发芽的粒数的分布列及平均数.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    篮球运动员在比赛中每次罚球命中得1分，罚不中得0分，已知某运动员罚球命中的概率为0.7，则他罚球2次（每次罚球结果互不影响）的得分的数学期望是       ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

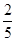    （本大题9分）袋中有2个红球，n个白球，各球除颜色外均相同.已知从袋中摸出2个球均为白球的概率为，（Ⅰ）求n；（Ⅱ）从袋中不放回的依次摸出三个球，记ξ为相邻两次摸出的球不同色的次数（例如：若取出的球依次为红球、白球、白球，则ξ=1），求随机变量ξ的分布列及其数学期望Eξ.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

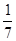    （本题10分）袋中有红、白两种颜色的小球共7个，它们除颜色外完全相同，从中任取2个，都是白色小球的概率为，甲、乙两人不放回地从袋中轮流摸取一个小球，甲先取，乙后取，然后再甲取……，直到两人中有一人取到白球时游戏停止，用X表示游戏停止时两人共取小球的个数。
    （1）求；
    （2）求。

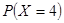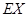    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    .随机变量的概率分布率由下图给出：

    则随机变量的均值是        

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设是离散型随机变量，，，且a<b，又Eξ=，Dξ=，则a+b的值为（  ）
    A．B．C．3 D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知某随机变量X的分布列如下（）：

    则随机变量X的数学期望=_______，方差=____________.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知离散型随机变量的分布列如右表．若，，则        ，       ．

    查看答案和解析>>

    同步练习册答案