
���� ��1��������ɵ�c=1�������õ�f��x������ȡg��x��=x��
��2��������ڳ���a��b��c�������⣬��x=1���ɵ�a+b+c=1�����ɶ��β���ʽ���������ⷨ�������б�ʽС�ڵ���0�����������������жϴ��ڣ�
��� �⣺��1������f��x��=ax2+bx+c��ͼ���㣨-1��0����
�ɵ�a-b+c=0����a=1��b=2��
��f��x��=x2+2x+1��
���¶���ɵ�g��x��=xΪ����f��x����һ�����к�����
��2��������ڳ���a��b��c��ʹ��y=xΪ����f��x����һ�����к�����
��f��x��Ϊ����$y=\frac{1}{2}{x^2}+\frac{1}{2}$��һ�����к�����
����x��ax2+bx+c��$\frac{1}{2}$x2+$\frac{1}{2}$�������
��x=1�ɵ�1��a+b+c��1����Ϊa+b+c=1��
��1-b=a+c��
��ax2+��b-1��x+c��0��������ɵ�a��0���ң�b-1��2-4ac��0��
����a+c��2-4ac��0������a=c��
�֣�a-$\frac{1}{2}$��x2+bx+c-$\frac{1}{2}$��0�������
�ɵ�a��$\frac{1}{2}$����b2-4��a-$\frac{1}{2}$����c-$\frac{1}{2}$����0��
����1-2a��2-4��a-$\frac{1}{2}$��2��0�������
�ʴ��ڳ���a��b��c����0��a=c��$\frac{1}{2}$��b=1-2a��
��ȡa=c=$\frac{1}{4}$��b=$\frac{1}{2}$���������⣮
���� ���⿼���¶������������ã����鲻��ʽ���������Ľⷨ��ע�����ø�ֵ�����б�ʽ�����������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
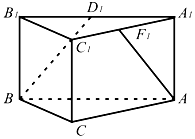 ��ͼ��ֱ������ABC-A1B1C1�У���BCA=90�㣬��D1��F1�ֱ���A1B1��A1C1���е㣬��BC=CA=2CC1����BD1��AF1���ɵĽ��ǣ�������
��ͼ��ֱ������ABC-A1B1C1�У���BCA=90�㣬��D1��F1�ֱ���A1B1��A1C1���е㣬��BC=CA=2CC1����BD1��AF1���ɵĽ��ǣ�������| A�� | 30�� | B�� | 45�� | C�� | 60�� | D�� | 90�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֱ��ͬһ��ֱ�ߵ�����ֱ�����ֱ | |
| B�� | ��һ��ֱ��ƽ���������ཻƽ�棬������ֱ����������ƽ��Ľ���ƽ�� | |
| C�� | ��һ��ƽ�澭����һ��ƽ��Ĵ��ߣ���ô������ƽ�����ֱ | |
| D�� | ��һ��ƽ���ڵ������ֱཻ������һ��ƽ���ڵ��ֱཻ�߷ֱ�ƽ�У���ô������ƽ���ƽ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��4�� | B�� | ��0��4] | C�� | [0��4�� | D�� | [0��4] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��Բ�ĶԳ�����������ԭ�㣬һ������ΪA��0��2�����ҽ���F���$B��\sqrt{2}��\sqrt{2}��$�ľ���Ϊ2��
��Բ�ĶԳ�����������ԭ�㣬һ������ΪA��0��2�����ҽ���F���$B��\sqrt{2}��\sqrt{2}��$�ľ���Ϊ2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABC-A1B1C1�У�����߳�Ϊa�����ⳤΪ$\frac{{\sqrt{2}}}{2}a$���������Խ���AB1����Խ���BC1ƽ�е�ƽ�潻�ϵ�����DB1��
��ͼ��������ABC-A1B1C1�У�����߳�Ϊa�����ⳤΪ$\frac{{\sqrt{2}}}{2}a$���������Խ���AB1����Խ���BC1ƽ�е�ƽ�潻�ϵ�����DB1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��{0��\frac{1}{2}}��$ | B�� | $��{\frac{1}{2}��1}��$ | C�� | ��1��2�� | D�� | ��2��3�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com