
设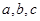 为三角形
为三角形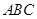 的三边,求证:
的三边,求证: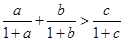
见解析
解析试题分析:本题用直接法不易找到证明思路,用分析法,要证该不等式成立,因为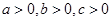 ,所以
,所以 ,只需证该不等式两边同乘以
,只需证该不等式两边同乘以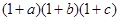 转化成的等价不等式a(1+b)(1+c)+ b(1+a)(1+c)> c(1+a)(1+b)成立,用不等式性质整理为a+2ab+b+abc>c成立,用不等式性质及三角不等式很容易证明此不等式成立.
转化成的等价不等式a(1+b)(1+c)+ b(1+a)(1+c)> c(1+a)(1+b)成立,用不等式性质整理为a+2ab+b+abc>c成立,用不等式性质及三角不等式很容易证明此不等式成立.
试题解析:要证明: 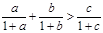
需证明: a(1+b)(1+c)+ b(1+a)(1+c)> c(1+a)(1+b) 5分
需证明:a(1+b+c+bc)+ b(1+a+c+ac)> c(1+a+b+ab) 需证明a+2ab+b+abc>c 10分
∵a,b,c是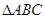 的三边 ∴a>0,b>0,c>0且a+b>c,abc>0,2ab>0
的三边 ∴a>0,b>0,c>0且a+b>c,abc>0,2ab>0
∴a+2ab+b+abc>c
∴ 成立。 14分
成立。 14分
考点:分析法证明不等式;三角形两边之和大于第三边.


科目:高中数学 来源: 题型:解答题
在某两个正数x,y之间,若插入一个数a,使x,a,y成等差数列,若插入两个数b,c,使x,b,c,y成等比数列,求证:(a+1)2≥(b+1)(c+1).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com