
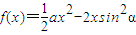 和函数g(x)=lnx,记F(x)=f(x)+g(x).
和函数g(x)=lnx,记F(x)=f(x)+g(x).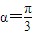 时,若f(x)在[1,2]上的最大值是f(2),求实数a的取值范围;
时,若f(x)在[1,2]上的最大值是f(2),求实数a的取值范围;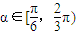 ,若F(x)在其定义域内既有极大值又有极小值,试求实数a的取值范围.
,若F(x)在其定义域内既有极大值又有极小值,试求实数a的取值范围.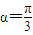 时求出函数
时求出函数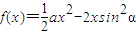 的解析式,利用导数研究出函数在[1,2]上的单调性,及最大值是f(2),建立不等式解出实数a的取值范围;
的解析式,利用导数研究出函数在[1,2]上的单调性,及最大值是f(2),建立不等式解出实数a的取值范围;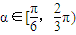 ,若F(x)在其定义域内既有极大值又有极小值,可得出其导数在定义域上恒有两个不同的根,解出函数的导数,根据其形式选择合适的方法将导数为0有两个不同根转化为关于参数的不等式,求解.
,若F(x)在其定义域内既有极大值又有极小值,可得出其导数在定义域上恒有两个不同的根,解出函数的导数,根据其形式选择合适的方法将导数为0有两个不同根转化为关于参数的不等式,求解.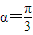 时,
时,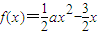 .
.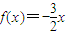 ,不合题意;
,不合题意;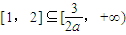
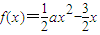 在
在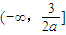 上递增,在
上递增,在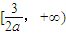 上递减,而,故不合题意;
上递减,而,故不合题意;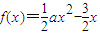 在
在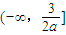 上递减,在
上递减,在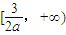 上递增,
上递增, ,所以a≥1.
,所以a≥1.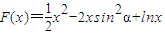 定义域为(0,+∞),
定义域为(0,+∞),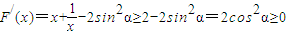 .
.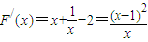 ,令F′(x)=0有x=1,但是x∈(0,1)时,F′(x)>0,F(x)单调递增,x∈(1,+∞)时,F′(x)>0,F(x)也单调递增,所以F(x)在其定义域内也没有极值.
,令F′(x)=0有x=1,但是x∈(0,1)时,F′(x)>0,F(x)单调递增,x∈(1,+∞)时,F′(x)>0,F(x)也单调递增,所以F(x)在其定义域内也没有极值.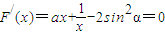 ,即方程ax2-2xsin2α+1=0在(0,+∞)上恒有两个不相等的实数根.即
,即方程ax2-2xsin2α+1=0在(0,+∞)上恒有两个不相等的实数根.即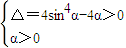 恒成立,因为
恒成立,因为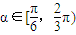 ,
,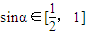 ,所以
,所以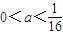 .
.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
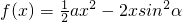 和函数g(x)=lnx,记F(x)=f(x)+g(x).
和函数g(x)=lnx,记F(x)=f(x)+g(x). 时,若f(x)在[1,2]上的最大值是f(2),求实数a的取值范围;
时,若f(x)在[1,2]上的最大值是f(2),求实数a的取值范围;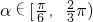 ,若F(x)在其定义域内既有极大值又有极小值,试求实数a的取值范围.
,若F(x)在其定义域内既有极大值又有极小值,试求实数a的取值范围.查看答案和解析>>
科目:高中数学 来源:2010-2011学年底江苏省连云港市赣榆高级中学高三(下)摸底数学试卷(解析版) 题型:解答题
 和函数g(x)=lnx,记F(x)=f(x)+g(x).
和函数g(x)=lnx,记F(x)=f(x)+g(x). 时,若f(x)在[1,2]上的最大值是f(2),求实数a的取值范围;
时,若f(x)在[1,2]上的最大值是f(2),求实数a的取值范围; ,若F(x)在其定义域内既有极大值又有极小值,试求实数a的取值范围.
,若F(x)在其定义域内既有极大值又有极小值,试求实数a的取值范围.查看答案和解析>>
科目:高中数学 来源:2010年江苏省南通市通州区高三4月模拟数学试卷(解析版) 题型:解答题
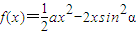 和函数g(x)=lnx,记F(x)=f(x)+g(x).
和函数g(x)=lnx,记F(x)=f(x)+g(x).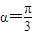 时,若f(x)在[1,2]上的最大值是f(2),求实数a的取值范围;
时,若f(x)在[1,2]上的最大值是f(2),求实数a的取值范围;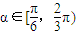 ,若F(x)在其定义域内既有极大值又有极小值,试求实数a的取值范围.
,若F(x)在其定义域内既有极大值又有极小值,试求实数a的取值范围.查看答案和解析>>
科目:高中数学 来源:2011年上海市黄浦区大同中学高考数学三模试卷(文理合卷)(解析版) 题型:解答题
 和函数g(x)=2x-2-x
和函数g(x)=2x-2-x 的奇偶性,并判断和证明y=lgh(x)在定义域上的单调性;
的奇偶性,并判断和证明y=lgh(x)在定义域上的单调性;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com