
分析 由题意可得T=2π是f(x)的一个周期,问题转化为f(x)在[0,2π)上的值域,求导数计算极值和端点值,比较可得.
解答 解:由题意可得T=2π是f(x)=2sinx+sin2x的一个周期,
故只需考虑f(x)=2sinx+sin2x在[0,2π)上的值域,
先来求该函数在[0,2π)上的极值点,
求导数可得f′(x)=2cosx+2cos2x
=2cosx+2(2cos2x-1)=2(2cosx-1)(cosx+1),
令f′(x)=0可解得cosx=$\frac{1}{2}$或cosx=-1,
可得此时x=$\frac{π}{3}$,π或$\frac{5π}{3}$;
∴y=2sinx+sin2x的最大值和最小值只能在点x=$\frac{π}{3}$,π或$\frac{5π}{3}$和边界点x=0中取到,
计算可得f($\frac{π}{3}$)=$\frac{3\sqrt{3}}{2}$,f(π)=0,f($\frac{5π}{3}$)=-$\frac{3\sqrt{3}}{2}$,f(0)=0,
∴函数的最小值为-$\frac{3\sqrt{3}}{2}$,最大值为$\frac{3\sqrt{3}}{2}$,即函数的值域为[-$\frac{3\sqrt{3}}{2}$,$\frac{3\sqrt{3}}{2}$].
故答案为:[-$\frac{3\sqrt{3}}{2}$,$\frac{3\sqrt{3}}{2}$]
点评 本题考查三角函数恒等变换,涉及导数法求函数区间的最值,属中档题.


科目:高中数学 来源: 题型:解答题
 如图,在周长为60πcm的圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B、C、D在圆周上.
如图,在周长为60πcm的圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B、C、D在圆周上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1]∪(0,1] | B. | (-∞,-1]∪[0,1] | C. | (0,1] | D. | (-∞,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
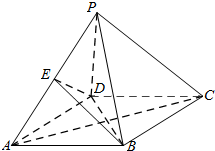 如图,四棱锥P-ABCD中,底面ABCD是边长为 4的菱形,PD=PB=4,∠BAD=60°,E为PA中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为 4的菱形,PD=PB=4,∠BAD=60°,E为PA中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com