
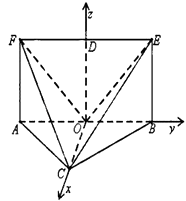
【题目】如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC.O为AB的中点,OF⊥EC. 
(1)求证:OE⊥FC:
(2)若 ![]() 时,求二面角F﹣CE﹣B的余弦值.
时,求二面角F﹣CE﹣B的余弦值.
【答案】
(1)证明:连结OC,∵AC=BC,O是AB的中点,
故OC⊥AB.
又∵平面ABC⊥平面ABEF,
故OC⊥平面ABE,于是OC⊥OF.
又OF⊥EC,∵OF⊥平面OEC,
∴OF⊥OE,
又∵OC⊥OE,∴OE⊥平面OFC,
∴OE⊥FC;
(2)解:由(1)得AB=2AF.不妨设AF=1,AB=2,
∵ ![]() ,∴AC=
,∴AC= ![]() ,则OC=
,则OC= ![]()
建立以O为坐标原点,OC,OB,OD分别为x,y,z轴的空间直角坐标系如图:
则F(0,﹣1,1),E(0,1,1),B(0,1,0),C( ![]() ,0,0),则
,0,0),则
![]() =(﹣
=(﹣ ![]() ,1,1),
,1,1), ![]() =(0,﹣2,0),
=(0,﹣2,0),
设平面FCE的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 ![]() .
.
∴ ![]() =(1,0,
=(1,0, ![]() ),
),
∵ ![]() =(0,0,1),
=(0,0,1), ![]() =(
=( ![]() ,﹣1,0),
,﹣1,0),
∴同理可得平面CEB的法向量为 ![]() =(1,
=(1, ![]() ,0),
,0),
∴cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() ,
,
∵二面角F﹣CE﹣B是钝二面角,
∴二面角F﹣CE﹣B的余弦值为﹣ ![]() .
.
【解析】(1)连结OC,则OC⊥AB,从而得到OC⊥OF,进而得到OF⊥OE,由此能证明OE⊥FC.(2)由(1)得AB=2AF.不妨设AF=1,AB=2建立空间坐标系,求出平面的法向量,利用向量法即可.
【考点精析】通过灵活运用直线与平面垂直的性质,掌握垂直于同一个平面的两条直线平行即可以解答此题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】(用空间向量坐标表示解答)已知正三棱柱ABC﹣A1B1C1的各棱长都是4,E是BC的中点,F在CC1上,且CF=1. 
(1)求证:EF⊥A1C;
(2)求二面角C﹣AF﹣E的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣t|+ ![]() (x>0);
(x>0);
(1)判断函数y=f(x)在区间(0,t]上的单调性,并证明;
(2)若函数y=f(x)的最小值为与t无关的常数,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,当x∈[0,+∞)时,f(x)=2x﹣2,则不等式f(log2x)>0的解集为( )
A.(0, ![]() )
)
B.( ![]() ,1)∪(2,+∞)
,1)∪(2,+∞)
C.(2,+∞)
D.(0, ![]() )∪(2,+∞)
)∪(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() (其中常数a>0,且a≠1).
(其中常数a>0,且a≠1).
(1)当a=10时,解关于x的方程f(x)=m(其中常数m>2 ![]() );
);
(2)若函数f(x)在(﹣∞,2]上的最小值是一个与a无关的常数,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com