
分析 (1)利用二项式定理系数的性质,求出xn的系数,即可得到结论.
(2)利用已知关系式,求出等式两边的常数项系数,即可得到结果.
解答 解:(1)${C}_{m+n}^{k}$=${{C}_{m}^{0}C}_{n}^{k}$+${{C}_{m}^{1}C}_{n}^{k-1}$+…+${{C}_{m}^{k}C}_{n}^{0}$=${C}_{m+m}^{k}$.
证明:(2)考察等式(2+x+$\frac{1}{x}$)n=$\frac{(x+1)^{2n}}{{x}^{n}}$,
等式右边的常数项为:$\frac{{C}_{2n}^{n}{x}^{n}}{{x}^{n}}{=C}_{2n}^{n}$,
∵$(2+x+\frac{1}{x})^{n}={\sum_{i=0}^{n}C}_{n}^{r}$•2n-r(x+$\frac{1}{x}$)r=${\sum_{i=0}^{n}C}_{n}^{r}$•2n-r(${\sum_{i=0}^{r}C}_{i}^{k}$$•{x}^{i-k}(\frac{1}{x})^{k})$,
当且仅当i=2k时,xr-k($\frac{1}{x}$)k为常数,
等式左边的常数项为:$\sum_{k=0}^{[{\frac{n}{2}}]}{C_n^{2k}}•{2^{n-2k}}•C_{2k}$k,
∴$\sum_{k=0}^{[{\frac{n}{2}}]}{C_n^{2k}}•{2^{n-2k}}•C_{2k}$k=Cnn成立.
点评 本题主要考查二项式定理等基础知识,考查推理论证能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥n,m⊥α,则n⊥α | B. | 若m∥α,m∥β,则α∥β | C. | 若m∥α,n∥α,则m∥n | D. | 若m∥α,α⊥β,则m⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{2}}}{81}π$ | B. | $\frac{{4\sqrt{5}}}{81}π$ | C. | $\frac{8}{81}π$ | D. | $\frac{10}{81}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
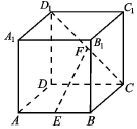 正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.
正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com