
【题目】已知函数f(x)=x|x﹣a|
(1)若函数y=f(x)+x在R上是增函数,求实数a的取值范围;
(2)若对任意x∈[1,2]时,函数f(x)的图像恒在y=1图像的下方,求实数a的取值范围;
(3)设a≥2时,求f(x)在区间[2,4]内的值域.
【答案】
(1)解:y=f(x)+x=x|a﹣x|+x= ![]()
由函数y=f(x)+x在R上是增函数,
则 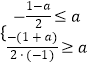 即﹣1≤a≤1,
即﹣1≤a≤1,
则a范围为﹣1≤a≤1
(2)解:由题意得对任意的实数x∈[1,2],f(x)<1恒成立,
即x|x﹣a|<1,当x∈[1,2]恒成立,即|a﹣x|< ![]() ,﹣
,﹣ ![]() <x﹣a<
<x﹣a< ![]() ,
,
即为x﹣ ![]() ,
,
故只要x﹣ ![]() 且a
且a ![]() 在x∈[1,2]上恒成立即可,
在x∈[1,2]上恒成立即可,
即有 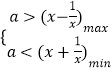 即
即 ![]()
(3)解:当a≥2时, ![]() ,f(x)=
,f(x)= ![]()
(Ⅰ)当 ![]() 即a>8时,f(x)在[2,4]上递增,f(x)min=f(2)=2a﹣4,f(x)max=f(4)=4a﹣16,∴值域为[2a﹣4,4a﹣16]
即a>8时,f(x)在[2,4]上递增,f(x)min=f(2)=2a﹣4,f(x)max=f(4)=4a﹣16,∴值域为[2a﹣4,4a﹣16]
(Ⅱ)当2≤ ![]() ≤4,及4≤a≤8时,f(x)=f(
≤4,及4≤a≤8时,f(x)=f( ![]() )=
)= ![]() ,f(2)﹣f(4)=12﹣2a
,f(2)﹣f(4)=12﹣2a
若4≤a<6,值域为[4a﹣16, ![]() ];若6≤a≤8,则值域为[2a﹣4,
];若6≤a≤8,则值域为[2a﹣4, ![]() ];
];
(Ⅲ)当1 ![]() ,即2≤a<4时f(x)min=0,且f(2)﹣f(4)=6﹣20,
,即2≤a<4时f(x)min=0,且f(2)﹣f(4)=6﹣20,
若2≤a< ![]() ,则值域为[0,16﹣4a].,若
,则值域为[0,16﹣4a].,若 ![]() ,则值域为[0,2a﹣4]
,则值域为[0,2a﹣4]
【解析】(1)y=f(x)+x=x|a﹣x|+x= ![]() ,要使函数y=f(x)+x在R上是增函数,只需
,要使函数y=f(x)+x在R上是增函数,只需 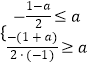 即可,(2)由题意得对任意的实数x∈[1,2],f(x)<1恒成立即可,(3)当a≥2时,
即可,(2)由题意得对任意的实数x∈[1,2],f(x)<1恒成立即可,(3)当a≥2时, ![]() ,f(x)=
,f(x)= ![]() ,根据二次函数的性质,分段求出值域即可.
,根据二次函数的性质,分段求出值域即可.
【考点精析】关于本题考查的函数的最值及其几何意义,需要了解利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能得出正确答案.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]()
![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,且当倾斜角为
两点,且当倾斜角为![]() 的直线
的直线![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() 时,有
时,有![]() .
.
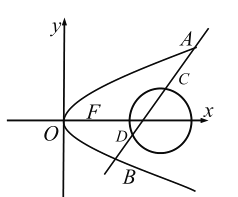
(1)求抛物线![]() 的方程;
的方程;
(2)已知圆![]() ,是否存在倾斜角不为
,是否存在倾斜角不为![]() 的直线
的直线![]() ,使得线段
,使得线段![]() 被圆
被圆![]() 截成三等分?若存在,求出直线
截成三等分?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :坐标系与参数方程选讲.
:坐标系与参数方程选讲.
在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ),曲线
),曲线![]()
![]() (
(![]() 为参数,实数
为参数,实数![]() ). 在以
). 在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点. 当
两点. 当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
(1)求![]() 的值; (2)求
的值; (2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某单位的职工食堂中,食堂每天以![]() 元/个的价格从面包店购进面包,然后以
元/个的价格从面包店购进面包,然后以![]() 元/个的价格出售.如果当天卖不完,剩下的面包以
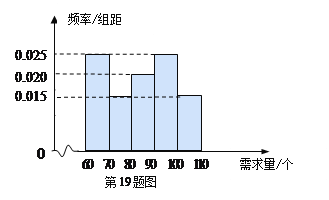
元/个的价格出售.如果当天卖不完,剩下的面包以![]() 元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了
元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了![]() 个面包,以
个面包,以![]() (单位:个,
(单位:个, ![]() )表示面包的需求量,
)表示面包的需求量, ![]() (单位:元)表示利润.
(单位:元)表示利润.
(Ⅰ)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅱ)求食堂每天面包需求量的中位数;
(Ⅲ)根据直方图估计利润![]() 不少于
不少于![]() 元的概率;
元的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为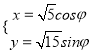 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为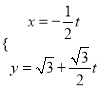 (
(![]() 为参数).以原点为极点,
为参数).以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,点
轴的正半轴为极轴建立极坐标系,点![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求点![]() 的直角坐标,并求曲线
的直角坐标,并求曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 的两个交点为
的两个交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了对生产的一种新产品进行合理定价,将该产品按事先拟定的价格进行试销,得到以下数据:
单价x(元/件) | 60 | 62 | 64 | 66 | 68 | 70 |
销量y(件) | 91 | 84 | 81 | 75 | 70 | 67 |
(I)画出散点图,并求![]() 关于
关于![]() 的回归方程;
的回归方程;
(II)已知该产品的成本是36元/件,预计在今后的销售中,销量与单价仍然服从(I)中的关系,为使企业获得最大利润,该产品的单价应定为多少元(精确到元)?
附:回归直线![]() 的斜率和截距的最小二乘法估计公式分别为:
的斜率和截距的最小二乘法估计公式分别为:
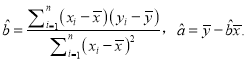
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com