
【题目】在平面直角坐标系中,设![]() 的顶点分别为
的顶点分别为![]() ,圆
,圆![]() 是
是![]() 的外接圆,直线
的外接圆,直线![]() 的方程是
的方程是![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)证明:直线![]() 与圆
与圆![]() 相交;
相交;
(3)若直线![]() 被圆
被圆![]() 截得的弦长为3,求
截得的弦长为3,求![]() 的方程.
的方程.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() 或
或![]() .
.
【解析】
(1)求出边AC、BC的垂直平分线方程,根据圆心M在这2条边的垂直平分线上,可得M(![]() ,
,![]() ),再求出半径MC的值,即可得到圆的标准方程.(2)根据直线l经过定点N,而点N在圆的内部,即可得到直线和圆相交.(3)由条件利用弦长公式求得圆心M(
),再求出半径MC的值,即可得到圆的标准方程.(2)根据直线l经过定点N,而点N在圆的内部,即可得到直线和圆相交.(3)由条件利用弦长公式求得圆心M(![]() ,
,![]() )到直线l的距离为d=
)到直线l的距离为d=![]() .再根据据点到直线的距离公式求得m的值,可得直线l的方程.
.再根据据点到直线的距离公式求得m的值,可得直线l的方程.
(1)∵△ABC的顶点分别为A(0,2),B(﹣1,0),C(2,0),故线段BC的垂直平分线方程为x=![]() ,
,
线段AC的垂直平分线为 y=x,再由圆心M在这2条边的垂直平分线上,可得M(![]() ,
,![]() ),
),
故圆的半径为|MC|=![]() =
=![]() ,故圆的方程为
,故圆的方程为![]() +
+![]() =
=![]() .
.
(2)根据直线l的方程是(2+m)x+(2m﹣1)y﹣3m﹣1=0(m∈R),即m(x+2y﹣3)+2x﹣y﹣1=0,
由![]() 可得
可得![]() ,故直线经过定点N(1,1).
,故直线经过定点N(1,1).
由于MN=![]() =
=![]() <r=
<r=![]() ,故点N在圆的内部,故圆和直线相交.
,故点N在圆的内部,故圆和直线相交.
(3)∵直线l被圆M截得的弦长为3,
故圆心M(![]() ,
,![]() )到直线l的距离为d=
)到直线l的距离为d=![]() =
=![]() .
.
再根据点到直线的距离公式可得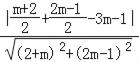 =
=![]() ,求得 m=﹣2,或m=
,求得 m=﹣2,或m=![]() ,
,
故直线l的方程为y=1或x=1.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】一个化肥厂生产甲种混合肥料1车皮、乙种混合肥料1车皮所需要的主要原料如表:
原料 | 磷酸盐(单位:吨) | 硝酸盐(单位:吨) |
甲 | 4 | 20 |
乙 | 2 | 20 |
现库存磷酸盐8吨、硝酸盐60吨,计划在此基础上生产若干车皮的甲、乙两种混合肥料.
(1)设x,y分别表示计划生产甲、乙两种肥料的车皮数,试列出x,y满足的数学关系式,并画出相应的平面区域;
(2)若生产1车皮甲种肥料,利润为3万元;生产1车皮乙种肥料,利润为2万元.那么分别生产甲、乙两种肥料多少车皮,能够产生最大利润?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 命题“若x2-4x+3=0,则x=3”的逆否命题是:“若x≠3,则x2-4x+3≠0”
B. “x>1”是“|x|>0”的充分不必要条件
C. 若p且q为假命题,则p、q均为假命题
D. 命题p:“x0∈R使得![]() +x0+1<0”,则
+x0+1<0”,则![]() p:“x∈R,均有x2+x+1≥0”
p:“x∈R,均有x2+x+1≥0”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() =(cosθ,sinθ),
=(cosθ,sinθ), ![]() =(﹣
=(﹣ ![]() ,
, ![]() );
);
(1)若 ![]() ∥
∥ ![]() ,且θ∈(0,π),求θ;
,且θ∈(0,π),求θ;
(2)若|3 ![]() +
+ ![]() |=|
|=| ![]() ﹣3
﹣3 ![]() |,求|
|,求| ![]() +
+ ![]() |的值.
|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若两直线![]() 的倾斜角分别为
的倾斜角分别为![]() 与
与![]() ,则下列四个命题中正确的是( )
,则下列四个命题中正确的是( )
A. 若![]() <
<![]() ,则两直线的斜率:k1 < k2 B. 若
,则两直线的斜率:k1 < k2 B. 若![]() =
=![]() ,则两直线的斜率:k1= k2
,则两直线的斜率:k1= k2
C. 若两直线的斜率:k1 < k2 ,则![]() <
<![]() D. 若两直线的斜率:k1= k2 ,则
D. 若两直线的斜率:k1= k2 ,则![]() =
=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com