
【题目】已知函数![]() 有两个不同的极值点.
有两个不同的极值点.
(Ⅰ)求实数a的取值范围;
(Ⅱ)若对任意![]() 存在
存在![]() 使得
使得![]() 成立,证明:
成立,证明:![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】
(Ⅰ)求得![]() ,令
,令![]() ,得到
,得到![]() ,设
,设![]() ,
,
利用导数求得函数![]() 的单调性与最值,列出不等式组,即可求解;
的单调性与最值,列出不等式组,即可求解;
(Ⅱ)由(Ⅰ)知![]() ,得到
,得到![]() ,把对任意
,把对任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,转化为
成立,转化为![]() ,化简
,化简 ,
,
令![]() ,利用导数求得函数
,利用导数求得函数![]() 的单调性与极值,即可求解.
的单调性与极值,即可求解.
(Ⅰ)由函数![]() ,则
,则 ,
,
令![]() ,可得
,可得![]() ,
,
设![]() ,则
,则![]() ,
,
令![]() ,解得
,解得![]() ,
,
列表如下:
|
|
|
|
| + | 0 | - |
| 单调递增 | 单调递减 |
所以![]() 的极大值为
的极大值为![]() ,
,
又因为![]() ,
,
所以函数![]() 有两个不同的极值点等价于
有两个不同的极值点等价于![]() ,解得
,解得![]() ,
,
因此实数![]() 的取值范围为
的取值范围为![]() ;
;
(Ⅱ)由(Ⅰ)知![]() ,故
,故![]() ,
,
设![]() 的较大零点为
的较大零点为![]() ,则
,则![]() ,
,
且![]() ,
,![]() ;
;![]() ,
,![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
从而![]() 有最大值为
有最大值为![]() ,
,
又当![]() 时,
时,![]() ,故可设函数
,故可设函数![]() 的值域为
的值域为![]() ,其中
,其中![]() ,
,
由题意:对任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,
成立,
等价于![]() ,
,
而![]() ,且
,且![]() ,
,
所以 ,
,![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,故
,故![]() ,
,
因此![]() .
.


科目:高中数学 来源: 题型:
【题目】新生儿某疾病要接种三次疫苗免疫(即0、1、6月龄),假设每次接种之间互不影响,每人每次接种成功的概率相等为了解新生儿该疾病疫苗接种剂量与接种成功之间的关系,现进行了两种接种方案的临床试验:10μg/次剂量组与20μg/次剂量组,试验结果如下:
接种成功 | 接种不成功 | 总计(人) | |
10μg/次剂量组 | 900 | 100 | 1000 |
20μg/次剂量组 | 973 | 27 | 1000 |
总计(人) | 1873 | 127 | 2000 |
(1)根据数据说明哪种方案接种效果好?并判断能否有99.9%的把握认为该疾病疫苗接种成功与两种接种方案有关?
(2)以频率代替概率,若选用接种效果好的方案,参与该试验的1000人的成功人数比此剂量只接种一次的成功人数平均提高多少人.
参考公式: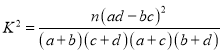 ,其中
,其中![]()
参考附表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
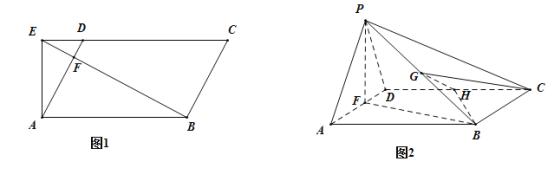
【题目】在平行四边形![]() 中,
中,![]() 过
过![]() 点作
点作![]() 的垂线交
的垂线交![]() 的延长线于点
的延长线于点![]() ,
,![]() .连结
.连结![]() 交
交![]() 于点
于点![]() ,如图1,将
,如图1,将![]() 沿
沿![]() 折起,使得点
折起,使得点![]() 到达点
到达点![]() 的位置.如图2.
的位置.如图2.
![]() 证明:直线
证明:直线![]()
![]() 平面
平面![]()
![]() 若
若![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,且平面
的中点,且平面![]() 平面
平面![]() 求三棱锥
求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=x3+ax2+bx+1的导数f′(x)满足f′(1)=2a,f′(2)=-b,其中常数a,b∈R.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)设g(x)=f′(x)e-x,求函数g(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的焦点坐标是![]() ,过点
,过点![]() 且垂直于长轴的直线交椭圆于
且垂直于长轴的直线交椭圆于![]() 两点,且
两点,且![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,问三角形
,问三角形![]() 内切圆面积是否存在最大值?若存在,请求出这个最大值及此时直线的方程;若不存在,请说明理由.
内切圆面积是否存在最大值?若存在,请求出这个最大值及此时直线的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
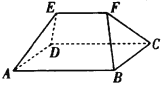
【题目】我国古代数学名著《九章算术》中记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”今有底面为正方形的屋脊形状的多面体(如图所示),下底面是边长为2的正方形,上棱![]() ,EF//平面ABCD,EF与平面ABCD的距离为2,该刍甍的体积为( )
,EF//平面ABCD,EF与平面ABCD的距离为2,该刍甍的体积为( )
A.6B.![]() C.
C.![]() D.12
D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com