
【题目】已知函数![]() (a<0).
(a<0).
(Ⅰ)当a=-3时,求f(x)的单调递减区间;
(Ⅱ)若函数f(x)有且仅有一个零点,求实数a的取值范围;
【答案】(1) 单调递减区间为(-3,-2)和(0,+∞);(2) a<0.
【解析】试题分析:(1)解关于导函数的不等式,得到所求的单调减区间;(2)函数f(x)有且仅有一个零点,即函数图象与x轴有唯一的公共点,利用导函数研究函数图象走势即可.
试题解析:
(Ⅰ)∵a=-3,∴![]() ,故
,故![]()
令f′(x)<0,解得-3<x<-2或x>0,
即所求的单调递减区间为(-3,-2)和(0,+∞)
(Ⅱ)∵![]() (x>a)
(x>a)
令f′(x)=0,得x=0或x=a+1
(1)当a+1>0,即-1<a<0时,f(x)在(a,0)和(a+1,+∞)上为减函数,在(0,a+1)上为增函数.
由于f(0)=aln(-a)>0,当x→a时,f(x)→+∞.
当x→+∞时,f(x)→-∞,于是可得函数f(x)图像的草图如图,
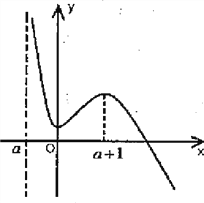
此时函数f(x)有且仅有一个零点.
即当-1<a<0对,f(x)有且仅有一个零点;
(2)当a=-1时,![]() ,
,
∵![]() ,∴f(x)在(a,+∞)单调递减,
,∴f(x)在(a,+∞)单调递减,
又当x→-1时,f(x)→+∞.当x→+∞时,f(x)→-∞,
故函数f(x)有且仅有一个零点;
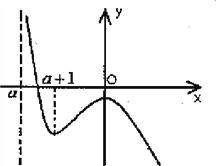
(3)当a+1<0即a<-1时,f(x)在(a,a+1)和(0,+∞)上为减函数,在(a+1,0)上为增函数.又f(0)=aln(-a)<0,当x→a时,f(x)→+∞,当x→+∞时,f(x)→-∞,于是可得函数f(x)图像的草图如图,此时函数f(x)有且仅有一个零点;
综上所述,所求的范围是a<0.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】祖暅原理:“幂势既同,则积不容异”.它是中国古代一个涉及几何体体积的问题,意思是两个同高的几何体,如在等高处的截面积恒相等,则体积相等.设![]() 为两个同高的几何体,
为两个同高的几何体,![]() 的体积不相等,
的体积不相等,![]() 在等高处的截面积不恒相等,根据祖暅原理可知,
在等高处的截面积不恒相等,根据祖暅原理可知,![]() 是
是![]() 的( )
的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x元与日销售量y件之间有如下所表示的关系.
x | … | 30 | 40 | 45 | 50 | … |
y | … | 60 | 30 | 15 | 0 | … |
(1)在所给的坐标系中,如图,根据表格提供的数据描出实数对(x,y)的对应点,并确定y与x的一个函数关系式y=f(x);
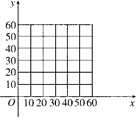
(2)设经营此商品的日销售利润为P元,根据上述关系,写出P关于x的函数关系式,并指出销售单价x为多少时,才能获得最大日销售利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
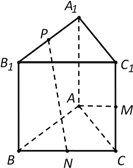
【题目】如图,直三棱柱ABC-A1B1C1中, AB=AC=AA1,AB⊥AC,M是CC1的中点,N是BC的中点,点P在线段A1B1上运动.
(Ⅰ)求证:PN⊥AM;
(Ⅱ)试确定点P的位置,使直线PN和平面ABC所成的角
最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com