
【题目】如图,在四棱锥P﹣ABCD中,四边形ABCD为平行四边形,AC,BD相交于点O,点E为PC的中点,OP=OC,PA⊥PD.求证: 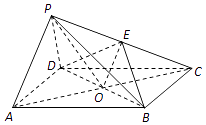
(1)直线PA∥平面BDE;
(2)平面BDE⊥平面PCD.
【答案】
(1)证明:连结OE,因为O为平行四边形ABCD对角线的交点,所以O为AC中点.
又因为E为PC的中点,
所以OE∥PA.
又因为OE平面BDE,PA平面BDE,
所以直线PA∥平面BDE
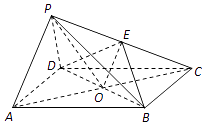
(2)证明:因为OE∥PA,PA⊥PD,所以OE⊥PD.
因为OP=OC,E为PC的中点,所以OE⊥PC.
又因为PD平面PCD,PC平面PCD,PC∩PD=P,
所以OE⊥平面PCD.
又因为OE平面BDE,所以平面BDE⊥平面PCD..
【解析】(1)连结OE,说明OE∥PA.然后证明PA∥平面BDE.(2)证明OE⊥PD.OE⊥PC.推出OE⊥平面PCD.然后证明平面BDE⊥平面PCD.
【考点精析】本题主要考查了直线与平面平行的判定和平面与平面垂直的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】为调查乘客的候车情况,公交公司在某为台的![]() 名候车乘客中随机抽取
名候车乘客中随机抽取![]() 人,将他们的候车时间(单位:分钟)作为样本分成
人,将他们的候车时间(单位:分钟)作为样本分成![]() 组,如下表所示:
组,如下表所示:
组别 | 候车时间 | 人数 |
一 |
|
|
二 |
|
|
三 |
|
|
四 |
|
|
五 |
|
|
(1)求这![]() 名乘客的平均候车时间;
名乘客的平均候车时间;
(2)估计这![]() 名候车乘客中候车时间少于
名候车乘客中候车时间少于![]() 分钟的人数;
分钟的人数;
(3)若从上表第三、四组的![]() 人中随机抽取
人中随机抽取![]() 人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区内有两条互相垂直的道路![]() 与
与![]() ,分别以
,分别以![]() 、
、![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴建立如图所示的平面直角坐标系
轴建立如图所示的平面直角坐标系![]() ,其第一象限有一块空地
,其第一象限有一块空地![]() ,其边界
,其边界![]() 是函数
是函数![]() 的图象,前一段曲线
的图象,前一段曲线![]() 是函数
是函数![]() 图象的一部分,后一段
图象的一部分,后一段![]() 是一条线段.测得
是一条线段.测得![]() 到
到![]() 的距离为
的距离为![]() 米,到
米,到![]() 的距离为
的距离为![]() 米,
米,![]() 长为
长为![]() 米.现要在此地建一个社区活动中心,平面图为梯形
米.现要在此地建一个社区活动中心,平面图为梯形![]() (其中点
(其中点![]() 在曲线
在曲线![]() 上,点
上,点![]() 在线段
在线段![]() 上,且
上,且![]() 、
、![]() 为两底边).
为两底边).
(1)求函数![]() 的解析式;
的解析式;
(2)当梯形的高为多少米时,该社区活动中心的占地面积最大,并求出最大面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
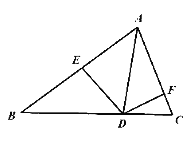
【题目】在锐角![]() 中,已知
中,已知![]() ,
,![]() ,若点
,若点![]() 是线段
是线段![]() 上一点(不含端点),过
上一点(不含端点),过![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() .
.
(1)若![]() 外接圆的直径长为
外接圆的直径长为![]() ,求
,求![]() 的值;
的值;
(2)求![]() 的最小值
的最小值
(3)问点![]() 在何处时,
在何处时,![]() 的面积最大?最大值为多少?
的面积最大?最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校将从4名男生和4名女生中选出4人分别担任辩论赛中的一、二、三、四辩手,其中男生甲不适合担任一辩手,女生乙不适合担任四辩手.现要求:如果男生甲入选,则女生乙必须入选.那么不同的组队形式有_________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ln(a x)+bx在点(1,f(1))处的切线是y=0;
(I)求函数f(x)的极值;
(II)当![]() 恒成立时,求实数m的取值范围(e为自然对数的底数)
恒成立时,求实数m的取值范围(e为自然对数的底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将参加数学竞赛决赛的500名同学编号为:001,002,…,500,采用系统抽样的方法抽取一个容量为50的样本,且随机抽的号码为003,这500名学生分别在三个考点考试,从001到200在第一考点,从201到355在第二考点,从356到500在第三考点,则第二考点被抽中的人数为( )
A.14
B.15
C.16
D.17
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系![]() 的原点为极点,
的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.若直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.若直线![]() 的参数方程为
的参数方程为![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(II)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() 点的直角坐标为
点的直角坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com