
【题目】如图,四边形ABCD为菱形,四边形ACFE为平行四边形,设BD与AC相交于点G,AB=BD=AE=2,∠EAD=∠EAB.

(1)证明:平面ACFE⊥平面ABCD;
(2)若直线AE与BC的夹角为60°,求直线EF与平面BED所成角的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)先由已知条件求得![]() ,得到
,得到![]() ,再结合菱形的对角线垂直,可得
,再结合菱形的对角线垂直,可得![]() 平面
平面![]() ,即可证得平面ACFE⊥平面ABCD;
,即可证得平面ACFE⊥平面ABCD;
(2)建立空间直角坐标系,求得各点的坐标,设![]() 的坐标,根据条件求出
的坐标,根据条件求出![]() ,再求得直线的方向向量和平面的法向量,利用向量的夹角公式,即可求解.
,再求得直线的方向向量和平面的法向量,利用向量的夹角公式,即可求解.
(1)证明:连接EG,因为AB=BD=AE=2,∠EAD=∠EAB,
可得△EAD≌EAB,∴ED=EB.
∵G为BD的中点,所以EG⊥BD,因为四边形ABCD为菱形,∴AC⊥BD,
∴BD⊥平面ACEF,因为BD平面ABCD;
∴平面ACFE⊥平面ABCD;
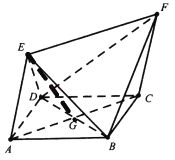
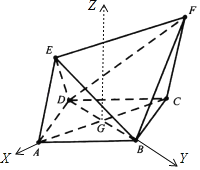
(2)因为EF∥AG,直线EF与平面BED所成角即为AG与平面BED所成角;
以G为原点建立如图所示空间直角坐标系,如图所示,
设E(a,0,b)则![]() (a
(a![]() ,0,b),
,0,b),
因为![]() (
(![]() ,﹣1,0),
,﹣1,0),
所以由条件可得:|![]() |2=(a
|2=(a![]() )2+b2=4且
)2+b2=4且![]()
![]() a+3=2×2×cos60°=2;
a+3=2×2×cos60°=2;
解得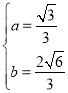 ,所以
,所以![]() (
(![]() ,﹣1,
,﹣1,![]() ),因为
),因为![]() (0,2,0);
(0,2,0);
所以可取平面BED的法向量![]() (2
(2![]() ,0,﹣1),因为
,0,﹣1),因为![]() (﹣2
(﹣2![]() ,0,0),
,0,0),
设直线EF与平面BED所成角为θ,则sinθ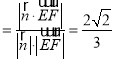 ,
,
∵0<θ![]() ;∴sosθ
;∴sosθ![]() ;
;
既直线EF与平面BED所成角的余弦值为![]() .
.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】某中学“主持朗诵”社团的成员中,分别有高一、高二、高三年级各1、2、3名表达与形象俱佳的学生,在该校“元旦节目汇演”中,要从这6名学生中选取两人担任节目主持人,则至少有一个是高三学生的概率是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程:在直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)已知点![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,它与曲线
,它与曲线![]() 的交点为
的交点为![]() ,
,![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)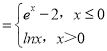 ,g(x)=f(
,g(x)=f(![]() )+1(k∈R,k≠0),则下列关于函数y=f[g(x)]+1的零点个数判断正确的是( )
)+1(k∈R,k≠0),则下列关于函数y=f[g(x)]+1的零点个数判断正确的是( )
A.当k>0时,有2个零点;当k<0时,有4个零点
B.当k>0时,有4个零点;当k<0时,有2个零点
C.无论k为何值,均有2个零点
D.无论k为何值,均有4个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为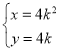 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)已知点![]() ,且直线
,且直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,人们的支付方式发生了巨大转变,使用移动支付购买商品已成为一部分人的消费习惯.某企业为了解该企业员工![]() 、
、![]() 两种移动支付方式的使用情况,从全体员工中随机抽取了100人,统计了他们在某个月的消费支出情况.发现样本中
两种移动支付方式的使用情况,从全体员工中随机抽取了100人,统计了他们在某个月的消费支出情况.发现样本中![]() ,
,![]() 两种支付方式都没有使用过的有5人;使用了
两种支付方式都没有使用过的有5人;使用了![]() 、
、![]() 两种方式支付的员工,支付金额和相应人数分布如下:
两种方式支付的员工,支付金额和相应人数分布如下:
支付金额(元) 支付方式 |
|
| 大于2000 |
使用 | 18人 | 29人 | 23人 |
使用 | 10人 | 24人 | 21人 |
依据以上数据估算:若从该公司随机抽取1名员工,则该员工在该月![]() 、
、![]() 两种支付方式都使用过的概率为______.
两种支付方式都使用过的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,射线
中,射线![]() 的方程为
的方程为![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() .一只小虫从点
.一只小虫从点![]() 沿射线
沿射线![]() 向上以
向上以![]() 单位/min的速度爬行
单位/min的速度爬行
(1)以小虫爬行时间![]() 为参数,写出射线
为参数,写出射线![]() 的参数方程;
的参数方程;
(2)求小虫在曲线![]() 内部逗留的时间.
内部逗留的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com