
| 2a |
| x |
| 2a |
| x |
| 50 |
| a |
| 2a |
| x |
| 2a |
| x |
| 2a |
| x |
| 50 |
| a |
| 50 |
| a |


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
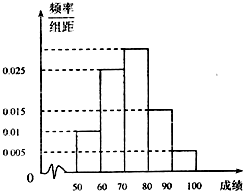 国家教育部要求高中阶段每学年都要组织学生进行“国家学生体质健康数据测试”,方案要求以学校为单位组织实施,某校对高一1班同学按照“国家学生体质健康数据测试”项目按百分制进行了测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
国家教育部要求高中阶段每学年都要组织学生进行“国家学生体质健康数据测试”,方案要求以学校为单位组织实施,某校对高一1班同学按照“国家学生体质健康数据测试”项目按百分制进行了测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、充分但非必要条件 |
| B、必要但非充分条件 |
| C、充要条件 |
| D、既非充分也非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| 2 |
| 1 |
| 4 |
| ||
| 4 |
| 3 |
| 4 |
| π |
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com