
【题目】如图,正四面体![]() 的顶点
的顶点![]() 分别在两两垂直的三条射线
分别在两两垂直的三条射线![]() 上,在下列命题中,错误的是( )
上,在下列命题中,错误的是( )

A. 四面体![]() 是正三棱锥 B. 直线
是正三棱锥 B. 直线![]() 与平面
与平面![]() 相交 C. 异面直线
相交 C. 异面直线![]() 和
和![]() 所成角是
所成角是![]() D. 直线
D. 直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]()
【答案】D
【解析】对于A,如图ABCD为正四面体,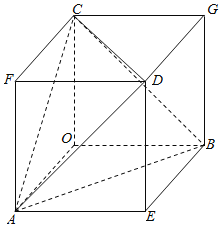
∴△ABC为等边三角形,
又∵OA、OB、OC两两垂直,∴OA⊥面OBC,∴OA⊥BC.
过O作底面ABC的垂线,垂足为N,连接AN交BC于M,
由三垂线定理可知BC⊥AM,∴M为BC中点,
同理可证,连接CN交AB于P,则P为AB中点,
∴N为底面△ABC中心,∴O﹣ABC是正三棱锥,
故A正确;
对于B,将正四面体ABCD放入正方体中,如图所示,
显然OB与平面ACD不平行.则B正确;
对于C,CD在平面ABC上的射影为![]() AC,
AC,
直线CD与平面ABC所成的角的正弦值为![]() ,故D错误;
,故D错误;
对于D,AB和OE垂直,且OE平行于CD,
则异面直线AB和CD所成的角为90°,
故C正确.
故选:D .


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
【题目】某景区修建一栋复古建筑,其窗户设计如图所示.圆![]() 的圆心与矩形
的圆心与矩形![]() 对角线的交点重合,且圆与矩形上下两边相切(
对角线的交点重合,且圆与矩形上下两边相切(![]() 为上切点),与左右两边相交(
为上切点),与左右两边相交(![]() ,
,![]() 为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1
为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1![]() ,且
,且![]() ,设
,设![]() ,透光区域的面积为
,透光区域的面积为![]() .
.

(1)求![]() 关于
关于![]() 的函数关系式,并求出定义域;
的函数关系式,并求出定义域;
(2)根据设计要求,透光区域与矩形窗面的面积比值越大越好.当该比值最大时,求边![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点、焦点在x轴上的椭圆,它的离心率为![]() ,且与直线x+y-1=0相交于M、N两点,若以MN为直径的圆经过坐标原点,求椭圆的方程.
,且与直线x+y-1=0相交于M、N两点,若以MN为直径的圆经过坐标原点,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:任意两个等边三角形都是相似的.
①它的否定是_________________________________________________________;
②否命题是_____________________________________________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年3月14日,“![]() 共享单车”终于来到芜湖,
共享单车”终于来到芜湖,![]() 共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于
共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于![]() ,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的
,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的![]() 名市民,并根据这
名市民,并根据这![]() 名市民对该项目满意程度的评分(满分
名市民对该项目满意程度的评分(满分![]() 分),绘制了如下频率分布直方图:
分),绘制了如下频率分布直方图:

(I)为了了解部分市民对“共享单车”评分较低的原因,该部门从评分低于![]() 分的市民中随机抽取
分的市民中随机抽取![]() 人进行座谈,求这
人进行座谈,求这![]() 人评分恰好都在
人评分恰好都在![]() 的概率;
的概率;
(II)根据你所学的统计知识,判断该项目能否通过考核,并说明理由.
(注:满意指数=![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究学生的数学核素养与抽象(能力指标![]() )、推理(能力指标
)、推理(能力指标![]() )、建模(能力指标
)、建模(能力指标![]() )的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标
)的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标![]() 的值评定学生的数学核心素养;若
的值评定学生的数学核心素养;若![]() ,则数学核心素养为一级;若
,则数学核心素养为一级;若![]() ,则数学核心素养为二级;若
,则数学核心素养为二级;若![]() ,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下结果:
,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下结果:
学生编号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)在这10名学生中任取两人,求这两人的建模能力指标相同的概率;
(2)从数学核心素养等级是一级的学生中任取一人,其综合指标为![]() ,从数学核心素养等级不是一级的学生中任取一人,其综合指标为
,从数学核心素养等级不是一级的学生中任取一人,其综合指标为![]() ,记随机变量
,记随机变量![]() ,求随机变量
,求随机变量![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌电视生产厂家有A,B两种型号的电视机参加了家电下乡活动,若厂家对A,B两种型号的电视机的投放金额分别为p,q万元,农民购买电视机获得的补贴分别为![]() p,
p, ![]() ln q万元,已知A,B两种型号的电视机的投放总额为10万元,且A,B两种型号的电视机的投放金额均不低于1万元,请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出最大值.(精确到0.1,参考数据:ln 4≈1.4)
ln q万元,已知A,B两种型号的电视机的投放总额为10万元,且A,B两种型号的电视机的投放金额均不低于1万元,请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出最大值.(精确到0.1,参考数据:ln 4≈1.4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器由于使用时间较长,生产的零件有一些缺损.按不同转速生产出来的零件有缺损的统计数据如下表所示:
转速x(转/秒) | 16 | 4 | 12 | 8 |
每小时生产有缺损零件数y(个) | 11 | 9 | 8 | 5 |
(1)作出散点图;
(2)如果y与x线性相关,求出回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么,机器的运转速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AC⊥BC,E、F分别在线段B1C1和AC上,B1E=3EC1 , AC=BC=CC1=4
(1)求证:BC⊥AC1;
(2)试探究满足EF∥平面A1ABB1的点F的位置,并给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com