
【题目】(本题满分12分)已知![]() ,函数
,函数![]()
(Ⅰ)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程.
处的切线方程.
(Ⅱ)若![]() ,求
,求![]() 在闭区间
在闭区间![]() 上的最小值.
上的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) .
.
【解析】试题分析:本题主要考查导数的运算、利用导数判断函数的单调性、利用导数求函数的极值和最值、利用导数求函数的切线方程等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,将![]() 代入
代入![]() 中,对
中,对![]() 求导,
求导, ![]() 为切点的纵坐标,而
为切点的纵坐标,而![]() 是切线的斜率,最后利用点斜式写出直线方程;第二问,对
是切线的斜率,最后利用点斜式写出直线方程;第二问,对![]() 求导,令
求导,令![]() ,将
,将![]() 分成两部分:
分成两部分: ![]() 和
和![]() 进行讨论,讨论函数的单调性,利用单调性判断函数的最小值,综合所有情况,得到
进行讨论,讨论函数的单调性,利用单调性判断函数的最小值,综合所有情况,得到![]() 的解析式.
的解析式.
试题解析:定义域: ![]() ,
, ![]()
(Ⅰ)当![]() 时,
时, ![]() ,则
,则![]()
![]() ,则
,则![]()
∴![]() 在
在![]() 处切线方程是:
处切线方程是: ![]() ,即
,即![]() ,
,
(Ⅱ)![]() ,令
,令![]() ,得到
,得到![]() ,
, ![]()
①当![]() 时,
时, ![]() ,则有
,则有
| 0 |
|
|
|
|
|
|
|
| 0 |
| 0 |
| ||
| 0 |
| 极大 |
| 极小 |
|
|
则最小值应该由![]() 与
与![]() 中产生,
中产生,
当![]() 时,
时, ![]() ,此时
,此时![]() ;
;
当![]() 时,
时, ![]() ,此时
,此时![]() ,
,
②当![]() 时,
时, ![]() ,则有
,则有
| 0 |
|
|
|
|
|
| 0 |
| ||
| 0 |
| 极小 |
|
|
则![]() ,
,
综上所述:当![]() 时,
时, ![]() 在区间
在区间![]() 上的最小值
上的最小值
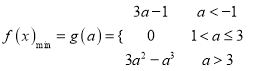


科目:高中数学 来源: 题型:
【题目】已知f(x)=sin2(2x﹣ ![]() )﹣2tsin(2x﹣
)﹣2tsin(2x﹣ ![]() )+t2﹣6t+1(x∈[
)+t2﹣6t+1(x∈[ ![]() ,
, ![]() ])其最小值为g(t).
])其最小值为g(t).
(1)求g(t)的表达式;
(2)当﹣ ![]() ≤t≤1时,要使关于t的方程g(t)=kt有一个实根,求实数k的取值范围.
≤t≤1时,要使关于t的方程g(t)=kt有一个实根,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为直角坐标系的坐标原点,双曲线
为直角坐标系的坐标原点,双曲线![]()
![]() 上有一点
上有一点![]() (
(![]() ),点
),点![]() 在
在![]() 轴上的射影恰好是双曲线
轴上的射影恰好是双曲线![]() 的右焦点,过点
的右焦点,过点![]() 作双曲线
作双曲线![]() 两条渐近线的平行线,与两条渐近线的交点分别为
两条渐近线的平行线,与两条渐近线的交点分别为![]() ,
, ![]() ,若平行四边形
,若平行四边形![]() 的面积为1,则双曲线的标准方程是( )
的面积为1,则双曲线的标准方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. 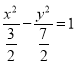
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA=![]() acosB.
acosB.
(1)求角B的大小;
(2)若b=3,sinC=2sinA,求a,c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an= ![]() (n∈N* , n≥2),数列{bn}满足关系式bn=
(n∈N* , n≥2),数列{bn}满足关系式bn= ![]() (n∈N*).
(n∈N*).
(1)求证:数列{bn}为等差数列;
(2)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1经过点A(﹣3,0),B(3,2),直线l2经过点B,且l1⊥l2 .
(1)求经过点B且在两坐标轴上的截距相等的直线的方程;
(2)设直线l2与直线y=8x的交点为C,求△ABC外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区某种农产品的年产量![]() (单位:吨)对价格
(单位:吨)对价格![]() (单位:千元/吨)和利润
(单位:千元/吨)和利润![]() 的影响,对近五年该农产品的年产量和价格统计如表:
的影响,对近五年该农产品的年产量和价格统计如表:
| 1 | 2 | 3 | 4 | 5 |
| 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润![]() 取到最大值?(保留两位小数)
取到最大值?(保留两位小数)
参考公式: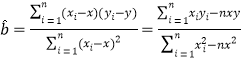 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com