
分析 先求出在同一个食堂就餐的概率,从而求出不在同一个食堂就餐的概率即可.
解答 解:三名学生选择每一个食堂的概率均为$\frac{1}{2}$,
则他们同时选中A食堂的概率为:$\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{8}$;
他们同时选中B食堂的概率也为:$\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{8}$;
故们在同一个食堂用餐的概率P=$\frac{1}{8}$+$\frac{1}{8}$=$\frac{1}{4}$,
故三个人不在同一个食堂就餐的概率是:$\frac{3}{4}$,
故答案为:$\frac{3}{4}$.
点评 本题考查了概率问题,作差即可,是一道基础题.


科目:高中数学 来源: 题型:解答题
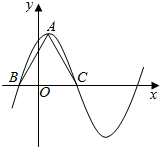 函数f(x)=3cos2$\frac{ωx}{2}$+$\frac{\sqrt{3}}{2}$sinωx-$\frac{3}{2}$(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为等边三角形.将函数f(x)的图象上各点的横坐标变为原来的π倍,将所得图象向右平移$\frac{2π}{3}$个单位,再向上平移1个单位,得到函数y=g(x)的图象
函数f(x)=3cos2$\frac{ωx}{2}$+$\frac{\sqrt{3}}{2}$sinωx-$\frac{3}{2}$(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为等边三角形.将函数f(x)的图象上各点的横坐标变为原来的π倍,将所得图象向右平移$\frac{2π}{3}$个单位,再向上平移1个单位,得到函数y=g(x)的图象查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | 14 | D. | 38 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥α,m⊥n,则n∥α | B. | 若m∥α,α⊥β,则m⊥β | ||
| C. | 若m∥α,n∥β,α⊥β,则m⊥n | D. | 若m⊥α,n⊥β,α⊥β,则m⊥n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 商品零售额 | 9.5 | 11.5 | 13.5 | 15.5 | 17.5 | 19.5 | 21.5 | 23.5 | 25.5 | 27.5 |
| 商品流通费率 | 6.0 | 4.6 | 4.0 | 3.2 | 2.8 | 2.5 | 2.4 | 2.3 | 2.2 | 2.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
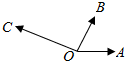 如图所示,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=$\sqrt{3}$,∠AOB=60°,$\overrightarrow{OB}$⊥$\overrightarrow{OC}$.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x,y的值分别是( )
如图所示,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=$\sqrt{3}$,∠AOB=60°,$\overrightarrow{OB}$⊥$\overrightarrow{OC}$.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x,y的值分别是( )| A. | -2,-1 | B. | -2,1 | C. | 2,-1 | D. | 2,1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$p | B. | 4$\sqrt{3}$p | C. | 6$\sqrt{3}$p | D. | 8$\sqrt{3}$p |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com