
分析 设g(x)=f(x)-$\frac{1}{3}$x,由f′(x)<$\frac{1}{3}$,得到g′(x)小于0,得到g(x)为减函数,将所求不等式变形后,利用g(x)为减函数求出x的范围,即为所求不等式的解集
解答 解:设g(x)=f(x)-$\frac{1}{3}$x,
∵f′(x)<$\frac{1}{3}$,
∴g′(x)=f′(x)-$\frac{1}{3}$<0,
∴g(x)为减函数,又f(2)=1,
∴f(log2x)>$\frac{lo{g}_{2}x+1}{3}$=$\frac{1}{3}$log2x+$\frac{1}{3}$,
即g(log2x)=f(log2x)-$\frac{1}{3}$log2x>$\frac{1}{3}$=g(2)=f(2)-$\frac{2}{3}$=g(log22),
∴log2x<log22,又y=log2x为底数是2的增函数,
∴0<x<2,
则不等式f(log2x)>$\frac{lo{g}_{2}x+1}{3}$的解集为(0,2).
故答案为:(0,2).
点评 此题考查了其他不等式的解法,涉及的知识有:利用导数研究函数的增减性,对数函数的单调性及特殊点,以及对数的运算性质,是一道综合性较强的试题


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2盏 | B. | 3盏 | C. | 4盏 | D. | 5盏 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
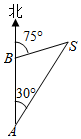 如图,一艘船下午13:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,14:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距9$\sqrt{2}$海里,则此船的航速为36海里/小时.
如图,一艘船下午13:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,14:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距9$\sqrt{2}$海里,则此船的航速为36海里/小时.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{8}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
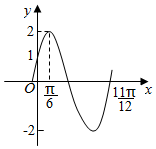 已知函数f(x)=Asin(ωx+φ),|φ|<$\frac{π}{2}$,图象如下,请回答下列问题.
已知函数f(x)=Asin(ωx+φ),|φ|<$\frac{π}{2}$,图象如下,请回答下列问题.查看答案和解析>>
科目:高中数学 来源:2016-2017学年内蒙古高二文上月考一数学试卷(解析版) 题型:解答题
已知椭圆 .
.
(Ⅰ)若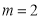 ,求椭圆
,求椭圆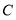 的离心率及短轴长;
的离心率及短轴长;
(Ⅱ)如存在过点 ,且与椭圆
,且与椭圆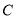 交于
交于 两点的直线
两点的直线 ,使得以线段
,使得以线段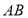 为直径的圆恰好通过坐标原点,求
为直径的圆恰好通过坐标原点,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com