
【题目】已知点A(1,﹣1),B(4,0),C(2,2),平面区域D是所有满足 ![]() =
= ![]() +μ
+μ ![]() (1<λ≤a,1<μ≤b)的点P(x,y)组成的区域.若区域D的面积为8,则4a+b的最小值为 ( )
(1<λ≤a,1<μ≤b)的点P(x,y)组成的区域.若区域D的面积为8,则4a+b的最小值为 ( )
A.5
B.4 ![]()
C.9
D.5+4 ![]()
【答案】C
【解析】解:如图所示,
延长AB到点N,延长AC到点M,使得|AN|=a|AB|,|AM|=b|AC|,作CH∥AN,BF∥AM,NG∥AM,MG∥AN,则四边形ABEC,ANGM,EHGF均为平行四边形.由题意可知:点P(x,y)组成的区域D为图中的四边形EFGH及其内部.
∵ ![]() =(3,1),
=(3,1), ![]() =(1,3),
=(1,3), ![]() =(﹣2,2),∴
=(﹣2,2),∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =2
=2 ![]() .
.
∴cos∠CAB= 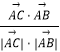 =
= ![]() =
= ![]() ,
, ![]() .
.
∴四边形EFGH的面积S= ![]() =8,
=8,
∴(a﹣1)(b﹣1)=1,即 ![]() .
.
∴4a+b=(4a+b) ![]() =5+
=5+ ![]()
![]() =9,当且仅当b=2a=3时取等号.
=9,当且仅当b=2a=3时取等号.
∴4a+b的最小值为9.
故选:C.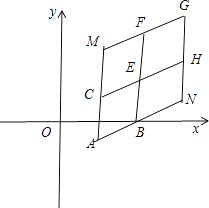
【考点精析】解答此题的关键在于理解基本不等式的相关知识,掌握基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() ,以及对平面向量的基本定理及其意义的理解,了解如果
,以及对平面向量的基本定理及其意义的理解,了解如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且
,且![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点(点
两点(点![]() 均在第一象限),且直线
均在第一象限),且直线![]() 的斜率成等比数列,证明:直线
的斜率成等比数列,证明:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分16分)
已知数列{an}的前n项和为Sn,且a1=1,Sn=n2an(n∈N*).
(1)试求出S1,S2,S3,S4,并猜想Sn的表达式;
(2)用数学纳法证明你的猜想,并求出an的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,按图所标边长,由勾股定理有:c2=a2+b2。设想正方形换成正方体,把截线换成如下图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O![]() LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是 .
LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,a,b,c分别为内角A,B,C的对边,2asin A=(2b+c)sin B+(2c+b)sin C.
且sin B+sin C=1,则△ABC是( )
A. 等腰钝角三角形 B. 等腰直角三角形 C. 钝角三角形 D. 直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2009四川卷文)设矩形的长为![]() ,宽为
,宽为![]() ,其比满足
,其比满足![]() ∶
∶![]() =
=![]() ,这种矩形给人以美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
,这种矩形给人以美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数,与标准值0.618比较,正确结论是
A. 甲批次的总体平均数与标准值更接近
B. 乙批次的总体平均数与标准值更接近
C. 两个批次总体平均数与标准值接近程度相同
D. 两个批次总体平均数与标准值接近程度不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com