
分析 由题意可知f(x)在D内是单调增函数,才为“成功函数”,由定义可构造loga(a2x+t)=x有两不同实数根,利用二次方程解出t的范围.
解答 解:∵g(x)=loga(a2x+t)(a>0且a≠1)是定义域为R的“成功函数”,
∴函数为增函数,且f(x)在[a,b]上的值域为[a,b],
∴g(a)=a,g(b)=b
∴相当于方程g(x)=x有两不同实数根,
∴loga(a2x+t)=x,得ax=a2x+t即a2x-ax+t=0
令m=ax,m>0
∴m2-m+t=0有两个不同的正数根,由韦达定理得,△=1-4t>0,t>0,1>0,
∴t∈(0,$\frac{1}{4}$).
故答案为:(0,$\frac{1}{4}$).
点评 本题主要考查对数函数的定义域和单调性,求函数的值域,难点在于构造函数,转化为两函数有不同二交点,利用方程解决.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
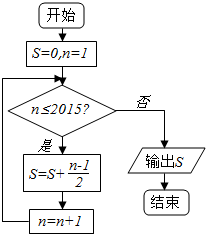
| A. | $\frac{2015×2016}{4}$ | B. | $\frac{2014×2015}{4}$ | C. | $\frac{2015×2016}{2}$ | D. | $\frac{2014×2015}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $-\frac{1}{8}$ | C. | $\frac{8}{17}$ | D. | $-\frac{8}{17}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $|{\overrightarrow a•\overrightarrow b}|≤|{\overrightarrow a}||{\overrightarrow b}|$ | B. | $|{\overrightarrow a-\overrightarrow b}|≤|{|{\overrightarrow a}|-|{\overrightarrow b}|}|$ | C. | ${(\overrightarrow a+\overrightarrow b)^2}={|{\overrightarrow a+\overrightarrow b}|^2}$ | D. | $(\overrightarrow a+\overrightarrow b)(\overrightarrow a-\overrightarrow b)={\overrightarrow a^2}-{\overrightarrow b^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com