
【题目】某市高中某学科竞赛中,某区![]() 名考生的参赛成绩的频率分布直方图如图所示.
名考生的参赛成绩的频率分布直方图如图所示.
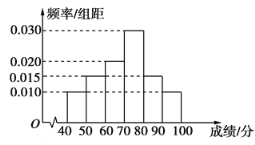
(1)求这![]() 名考生的平均成绩
名考生的平均成绩![]() (同一组中数据用该组区间中点值作代表);
(同一组中数据用该组区间中点值作代表);
(2)记![]() 分以上为合格,
分以上为合格,![]() 分及以下为不合格,结合频率分布直方图完成下表,能否在犯错误概率不超过
分及以下为不合格,结合频率分布直方图完成下表,能否在犯错误概率不超过![]() 的前提下认为该学科竞赛成绩与性别有关?
的前提下认为该学科竞赛成绩与性别有关?
不合格 | 合格 | 合计 | |
男生 |
| ||
女生 |
| ||
合计 |
|
附:
|
|
|
|
|
|
|
|
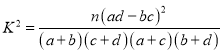 .
.
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,外接球的球心为
,外接球的球心为![]() ,点
,点![]() 是侧棱
是侧棱![]() 上的一个动点.有下列判断:①直线
上的一个动点.有下列判断:①直线![]() 与直线
与直线![]() 是异面直线;②
是异面直线;②![]() 一定不垂直于
一定不垂直于![]() ; ③三棱锥
; ③三棱锥![]() 的体积为定值;④
的体积为定值;④![]() 的最小值为
的最小值为![]() .其中正确的序号是______.
.其中正确的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
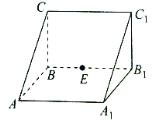
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起得到图(二),点
折起得到图(二),点![]() 为棱
为棱![]() 上的动点.
上的动点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,二面角
,二面角![]() 为
为![]() ,点
,点![]() 为
为![]() 中点,求二面角
中点,求二面角![]() 余弦值的平方.
余弦值的平方.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 山东省《体育高考方案》于2012年2月份公布,方案要求以学校为单位进行体育测试,某校对高三1班同学按照高考测试项目按百分制进行了预备测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
(Ⅰ)请估计一下这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成一个小组.若选出的两人成绩差大于20,则称这两人为“帮扶组”,试求选出的两人为“帮扶组”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
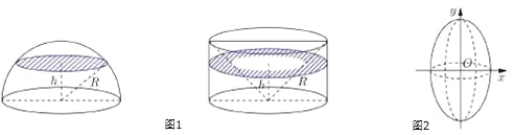
【题目】(数学文卷·2017届重庆十一中高三12月月考第16题) 现介绍祖暅原理求球体体积公式的做法:可构造一个底面半径和高都与球半径相等的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,用这样一个几何体与半球应用祖暅原理(图1),即可求得球的体积公式.请研究和理解球的体积公式求法的基础上,解答以下问题:已知椭圆的标准方程为![]() ,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解人们对“延迟退休年龄政策”的态度,某部门从年龄在15岁到65岁的人群中随机调查了100人,并得到如图所示的频率分布直方图,在这100人中不支持“延迟退休年龄政策”的人数与年龄的统计结果如表所示:


(1)由频率分布直方图,估计这100人年龄的平均数;
(2)根据以上统计数据填写下面的2![]() 2列联表,据此表,能否在犯错误的概率不超过5%的前提下,认为以45岁为分界点的不同人群对“延迟退休年龄政策”的态度存在差异?
2列联表,据此表,能否在犯错误的概率不超过5%的前提下,认为以45岁为分界点的不同人群对“延迟退休年龄政策”的态度存在差异?
45岁以下 | 45岁以上 | 总计 | |
不支持 | |||
支持 | |||
总计 |
参考数据:
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是平面内共始点的三个非零向量,且两两不共线,
是平面内共始点的三个非零向量,且两两不共线,![]() 有下列命题:
有下列命题:
(1)关于![]() 的方程
的方程![]() 可能有两个不同的实数解;
可能有两个不同的实数解;
(2)关于![]() 的方程
的方程![]() 至少有一个实数解;
至少有一个实数解;
(3)关于![]() 的方程
的方程![]() 最多有一个实数解;
最多有一个实数解;
(4)关于![]() 的方程
的方程![]() 若有实数解,则三个向量的终点不可能共线;
若有实数解,则三个向量的终点不可能共线;
上述命题正确的序号是__________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com