
【题目】已知函数f(x)=x2﹣2|x|﹣3a
(1)当a=1时,在所给坐标系中,画出函数f(x)的图象,并求f(x)的单调递增区间
(2)若直线y=1与函数f(x)的图象有4个交点,求a的取值范围.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】偶函数f(x)满足f(1﹣x)=f(1+x),且在x∈[0,1]时,f(x)= ![]() ,若直线kx﹣y+k=0(k>0)与函数f(x)的图象有且仅有三个交点,则k的取值范围是 .
,若直线kx﹣y+k=0(k>0)与函数f(x)的图象有且仅有三个交点,则k的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“累计净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为![]() 时对颗粒物的累计净化量(单位:克).根据国家标准,对空气净化器的累计净化量(CCM)有如下等级划分:
时对颗粒物的累计净化量(单位:克).根据国家标准,对空气净化器的累计净化量(CCM)有如下等级划分:
累计净化量(克) |
|
|
| 12以上 |
等级 |
|
|
|
|
已知某批空气净化器共![]() 台,其累计净化量都分布在区间
台,其累计净化量都分布在区间![]() 内,为了解其质量,随机抽取了
内,为了解其质量,随机抽取了![]() 台净化器作为样本进行估计,按照
台净化器作为样本进行估计,按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均匀分组,其中累计净化量在
均匀分组,其中累计净化量在![]() 的所有数据有:
的所有数据有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,并绘制了如下频率分布直方图.
,并绘制了如下频率分布直方图.
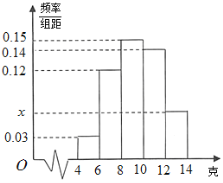
(1)求![]() 的值及频率分布直方图中
的值及频率分布直方图中![]() 的值;
的值;
(2)以样本估计总体,试估计这批空气净化器(共2000台)中等级为![]() 的空气净化器有多少台?
的空气净化器有多少台?
(3)从累计净化量在![]() 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3﹣2ax2+3x(x∈R).
x3﹣2ax2+3x(x∈R).
(1)若a=1,点P为曲线y=f(x)上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;
(2)若函数y=f(x)在(0,+∞)上为单调增函数,试求满足条件的最大整数a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=x2﹣2ax+3为定义在[﹣2,2]上的函数.
(1)当a=1时,求f(x)的最大值与最小值;
(2)若f(x)的最大值为M,最小值为m,函数g(a)=M﹣m,求g(a)的解析式,并求其最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)当a=2时,求f(x)在x∈[0,1]的最大值;
(2)当0<a<1,f(x)在x∈[0,1]上的最大值和最小值之和为a,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若二次函数![]() 的图象和直线
的图象和直线![]() 无交点,现有下列结论:
无交点,现有下列结论:
①方程![]() 一定没有实数根;②若
一定没有实数根;②若![]() ,则不等式
,则不等式![]() 对一切实数
对一切实数![]() 都成立;
都成立;
③若![]() ,则必存在实数
,则必存在实数![]() ,使
,使![]() ;④若
;④若![]() ,则不等式
,则不等式![]() 对一切实数都成立;⑤函数
对一切实数都成立;⑤函数![]() 的图象与直线
的图象与直线![]() 也一定没有交点,其中正确的结论是__________.(写出所有正确结论的编号)
也一定没有交点,其中正确的结论是__________.(写出所有正确结论的编号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com