
����Ŀ����֪����f��x��=asin2x+bcos2x��ab��0�����������ĸ����⣺������ȷ��������Ϊ������������ȷ�������ţ�
����a=1��b=�� ![]() ��Ҫ�õ�����y=f��x����ͼ��ֻ�轫����y=2sin2x��ͼ������ƽ��
��Ҫ�õ�����y=f��x����ͼ��ֻ�轫����y=2sin2x��ͼ������ƽ�� ![]() ����λ��
�����
����a=1��b=��1������y=f��x����һ���Գ�����Ϊ�� ![]() ,0����
,0����
����y=f��x����һ���Գ��᷽��Ϊx= ![]() ����a=b��
����a=b��
��������asin2x+bcos2x=m����ʵ������С�������ι���һ���Ȳ����У�������Ȳ����еĹ���Ϊ�У�
���𰸡��٢�
���������⣺���ڢ٣���a=1��b=�� ![]() ʱ��f��x��=sin2x��
ʱ��f��x��=sin2x�� ![]() cos2x=2sin��2x��
cos2x=2sin��2x�� ![]() ��=2sin2��x��
��=2sin2��x�� ![]() ����
����
Ҫ�õ�����y=f��x����ͼ��ֻ�轫����y=2sin2x��ͼ������ƽ�� ![]() ����λ��������ȷ��
����λ��������ȷ��
���ڢڣ���a=1��b=��1ʱ��f��x��=sin2x��cos2x= ![]() sin��2x��
sin��2x�� ![]() ����
����
��f�� ![]() ��=
��= ![]() sin��2��
sin��2�� ![]() ��
�� ![]() ��=1��0���ࣨ
��=1��0���ࣨ ![]() ��0�����Ǻ���y=f��x����һ���Գ����ģ�ԭ�������
��0�����Ǻ���y=f��x����һ���Գ����ģ�ԭ�������
���ڢۣ���y=f��x����һ���Գ��᷽��Ϊx= ![]() ʱ��
ʱ��
f�� ![]() ��=asin
��=asin ![]() +bcos
+bcos ![]() =
= ![]() a+
a+ ![]() b=
b= ![]() ��
��
�� ![]() ��a��b��2=0����a=b��������ȷ��
��a��b��2=0����a=b��������ȷ��
���ڢܣ���m=0ʱ������asin2x+bcos2x=m����ʵ������С�������ι���һ���Ȳ����У�
��ʱ�Ȳ����еĹ���Ϊ ![]() ��ԭ�������
��ԭ�������
���ϣ���ȷ�������Ǣ٢ۣ�
���Դ��ǣ��٢ۣ�
�����㾫����������Ĺؼ������������������ж���Ӧ�õ����֪ʶ�������������⻥Ϊ������⣬��������ͬ������ԣ���������Ϊ������������⣬���ǵ������û�й�ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������{an}��{bn}��ÿһ�����������a1=8��b1=16����an �� bn �� an+1�ɵȲ����У�bn �� an+1 �� bn+1�ɵȱ����У�
��1����a2 �� b2��ֵ��
��2��������{an}��{bn}��ͨ�ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ӣ�ÿ�����Ӷ�װ��4����ȫ��ͬ��С�����Ϸֱ��������1,2,3,4.
(1)�״�����һ������������һ�����Ҵ���һ����������һ����˭���������ϱ�����ִ�˭�ͻ�ʤ����������ͬ��Ϊƽ�֣������ʤ�ĸ��ʣ�
(2)�����루1��ͬ�����涨��������������������������ͬ��ʤ���������ֲ���ͬ���һ�ʤ�������涨��ƽ����˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ʱ������
ʱ������![]() �ĵ��������뼫ֵ��
�ĵ��������뼫ֵ��
��2����![]() ������
������![]() �IJ���ʽ
�IJ���ʽ![]() ���������
���������![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ⱥ�и���Ѫ�͵�����ռ�ı������£�
Ѫ�� | A | B | AB | O |
��Ѫ�͵�����ռ����(%) | 28 | 29 | 8 | 35 |
��֪ͬ��Ѫ�͵��˿�����Ѫ��O��Ѫ��������κ�һ��Ѫ�͵��ˣ�������ͬѪ�͵��˲��ܻ�����Ѫ��С����B��Ѫ����С������Ҫ��Ѫ���ʣ�
(1)����һ���ˣ���Ѫ�������С���ĸ����Ƕ��٣�
(2)����һ���ˣ���Ѫ�������С���ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ȤС�����о���ҹ�²��С�뻼��ð��������֮��Ĺ�ϵ,���Ƿֱ��������ijҽԺ��¼�� 1��6�·�ÿ��10�ŵ���ҹ�²��������ð�����������,�õ��������ϣ�
�� �� | 1��10�� | 2��10�� | 3��10�� | 4��10�� | 5��10�� | 6��10�� |
��ҹ�²�x(��C) | 10 | 11 | 13 | 12 | 8 | 6 |
��������y(��) | 22 | 25 | 29 | 26 | 16 | 12 |
����ȤС��ȷ�����о�������:�ȴ�������������ѡȡ2��,��ʣ�µ�4�����������Իع鷽��,���ñ�ѡȡ��2�����ݽ��м��飮
(1)��ѡȡ��2������ǡ�������������µĸ��ʣ�
(2)��ѡȡ����1����6�µ���������,�����2��5�·ݵ�����,���y����x�����Իع鷽��![]() ��
��
(3)�������Իع鷽�̵õ��Ĺ�����������ѡ���ļ������ݵ�����������2��,����Ϊ�õ������Իع鷽���������,���ʸ�С���������Իع鷽���Ƿ�����?
���ο�:����С���˷������Իع鷽��ϵ����ʽ 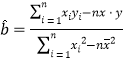 ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�۲�վ�ڸۿ�A����ƫ��40�㷽���C�������һ���ھ�۲�վ31�����B���������ŴӸۿڳ�����һ����ƫ��20��ĺ�������ۿ�A��ȥ����������20���ﵽ��D������ʱ�۲�վ�ֲ��CD����21����ʴ�ʱ����ۿ�A�����ж�Զ�� 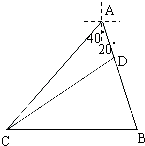
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������f��x��=sin2x��ͼ������ƽ�Ʀգ�0���գ� ![]() ������λ��õ�����g��x����ͼ����������|f��x1����g��x2��|=2��x1��x2��|x1��x2|min=
������λ��õ�����g��x����ͼ����������|f��x1����g��x2��|=2��x1��x2��|x1��x2|min= ![]() �����= ��
�����= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���ΪSn=��3n2+49n��
��1����������{an}�Ƿ�Ϊ�Ȳ����У�����ǣ���֤����
��2����bn=|an|��������{bn}��ǰn��ͣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com