
【题目】已知函数f(x)=a-![]() (a∈R).
(a∈R).
(1) 判断函数f(x)的单调性并给出证明;
(2) 若存在实数a使函数f(x)是奇函数,求a;
(3)对于(2)中的a,若f(x)≥![]() ,当x∈[2,3]时恒成立,求m的最大值.
,当x∈[2,3]时恒成立,求m的最大值.
【答案】(1)见解析;(2)a=1;(3)![]() .
.
【解析】试题分析:(1)设x1,x2∈R,且x1<x2,由定义法能推出f(x1)-f(x2)<0,从而得到f(x)在定义域上单调递增;
(2)由奇函数定义得f(0)=0,求参检验即可;
(3)由条件可得: m≤2x (1-![]() =(2x+1)+
=(2x+1)+![]() -3恒成立.m≤(2x+1)+
-3恒成立.m≤(2x+1)+![]() -3的最小值,x∈[2,3]即可得解.
-3的最小值,x∈[2,3]即可得解.
试题解析:
(1)不论a为何实数,f(x)在定义域上单调递增.
证明:设x1,x2∈R,且x1<x2,
则f(x1)-f(x2)=![]() -
-![]() =
=![]() .
.
由x1<x2可知0<2x1<2x2,
所以2x1-2x2<0,2x1+1>0,2x2+1>0,
所以f(x1)-f(x2)<0,f(x1)<f(x2).
所以由定义可知,不论a为何数,f(x)在定义域上单调递增.
(2)由f(0)=a-1=0得a=1,经验证,当a=1时,f(x)是奇函数.
(3)由条件可得: m≤2x![]() =(2x+1)+
=(2x+1)+![]() -3恒成立.m≤(2x+1)+
-3恒成立.m≤(2x+1)+![]() -3的最小值,x∈[2,3].
-3的最小值,x∈[2,3].
设t=2x+1,则t∈[5,9],函数g(t)=t+![]() -3在[5,9]上单调递增,
-3在[5,9]上单调递增,
所以g(t)的最小值是g(5)=![]() ,
,
所以m≤![]() ,即m的最大值是
,即m的最大值是![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
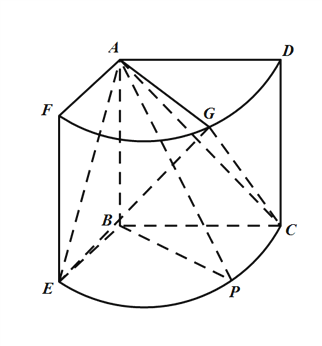
【题目】如图,几何体是圆柱的一部分,它是由矩形![]() (及其内部)以
(及其内部)以![]() 边所在直线为旋转轴旋转
边所在直线为旋转轴旋转![]() 得到的,
得到的, ![]() 是
是![]() 的中点.
的中点.
(![]() )设
)设![]() 是
是![]() 上的一点,且
上的一点,且![]() ,求
,求![]() 的大小;
的大小;
(![]() )当
)当![]() 时,求二面角
时,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,离心率为
,离心率为![]() .设过点
.设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同两点
相交于不同两点![]() ,
, ![]() 周长为
周长为![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知点![]() ,证明:当直线
,证明:当直线![]() 变化时,总有TA与
变化时,总有TA与![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:x∈A={x|x2﹣2x﹣3≤0,x∈R},q:x∈B={x|x2﹣2mx+m2﹣9≤0,x∈R,m∈R}.
(1)若A∩B=[1,3],求实数m的值;
(2)若p是q的充分条件,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com