
分析 求出条件p,q的等价条件,根据p是q的充分不必要条件,建立不等式关系即可.
解答 解:由1<2x<32得0<x<5,即q:0<x<5,
由k-2≤x-2≤k+2得k≤x≤k+4,即p:k≤x≤k+4,
若p是q的充分不必要条件,
则$\left\{\begin{array}{l}{k>0}\\{k+4<5}\end{array}\right.$,即$\left\{\begin{array}{l}{k>0}\\{k<1}\end{array}\right.$得0<k<1,
即实数k的取值范围是(0,1).
点评 本题主要考查充分条件和必要条件的应用,根据不等式的性质求解条件的等价条件是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{2π}{9}$个单位 | B. | 向左平移$\frac{2π}{9}$个单位 | ||
| C. | 向右平移$\frac{2π}{3}$个单位 | D. | 向左平移$\frac{2π}{3}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
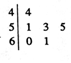 为了检查某高三毕业班学生的体重情况,从该班随机抽取了6位学生进行称重,如图为6位学生体重的茎叶图(单位:kg),其中图中左边是体重的十位数字,右边是个位数字,则这6位学生体重的平均数为( )
为了检查某高三毕业班学生的体重情况,从该班随机抽取了6位学生进行称重,如图为6位学生体重的茎叶图(单位:kg),其中图中左边是体重的十位数字,右边是个位数字,则这6位学生体重的平均数为( )| A. | 52 | B. | 53 | C. | 54 | D. | 55 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=2x | B. | f(x)=log${\;}_{\frac{1}{2}}$x | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=-x|x| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com