
在平面直角坐标系xOy中,已知椭圆C的中心在原点O,焦点在x轴上,短轴长为2,离心率为 .
.
(1)求椭圆C的方程;
(2)A,B为椭圆C上满足△AOB的面积为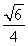 的任意两点,E为线段AB的中点,射线OE交椭圆C于点P.设
的任意两点,E为线段AB的中点,射线OE交椭圆C于点P.设 =t
=t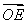 ,求实数t的值.
,求实数t的值.
(1) +y2=1(2)t=2或t=
+y2=1(2)t=2或t=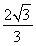
【解析】(1)设椭圆C的方程为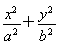 =1(a>b>0),
=1(a>b>0),
由题意知 解得
解得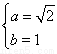
因此椭圆C的方程为 +y2=1.
+y2=1.
(2)(ⅰ)当A,B两点关于x轴对称时,设直线AB的方程为x=m.
由题意得-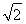 <m<0或0<m<
<m<0或0<m<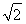 .
.
将x=m代入椭圆方程 +y2=1,得|y|=
+y2=1,得|y|= 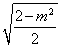 .
.
所以S△AOB=|m|·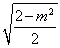 =
=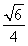 .解得m2=
.解得m2=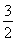 或m2=
或m2=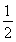 .①
.①
因为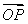 =t
=t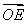 =
=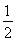 t(
t(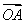 +
+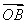 )=
)=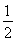 t(2m,0)=(mt,0),
t(2m,0)=(mt,0),
又P为椭圆C上一点,所以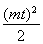 =1.②
=1.②
由①②,得t2=4或t2=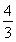 ,
,
又t>0,所以t=2或t=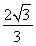 .
.
(ⅱ)当A,B两点关于x轴不对称时,设直线AB的方程为y=kx+h.
将其代入椭圆的方程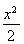 +y2=1,得
+y2=1,得
(1+2k2)x2+4khx+2h2-2=0.设A(x1,y1),B(x2,y2).
由判别式Δ>0可得1+2k2>h2,
此时x1+x2=-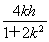 ,x1x2=
,x1x2=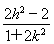 ,
,
y1+y2=k(x1+x2)+2h=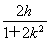 ,
,
所以|AB|=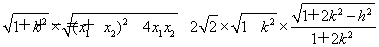 .
.
因为点O到直线AB的距离d=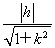 ,
,
所以S△AOB=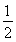 |AB|d=
|AB|d=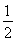 ×2
×2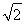 ×
×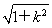 ×
×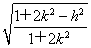 ×
×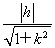 =
=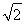 ×
×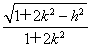 ×|h|.
×|h|.
又S△AOB=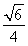 ,所以
,所以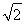 ×
×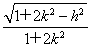 ×|h|=
×|h|=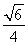 .③
.③
令n=1+2k2,代入③整理得3n2-16h2n+16h4=0.
解得n=4h2或n=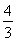 h2,即1+2k2=4h2或1+2k2=
h2,即1+2k2=4h2或1+2k2=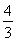 h2.④
h2.④
因为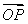 =t
=t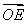 =
=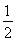 t(
t(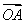 +
+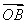 )=
)=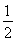 t(x1+x2,y1+y2)=
t(x1+x2,y1+y2)=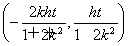 ,
,
又P为椭圆C上一点,
所以t2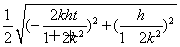 =1,即
=1,即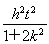 =1.⑤
=1.⑤
将④代入⑤,得t2=4或t2=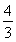 .
.
又t>0,故t=2或t=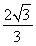 .
.
经检验,适合题意.
综合(ⅰ)(ⅱ),得t=2或t=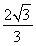


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集11讲练习卷(解析版) 题型:填空题
设x,y,z是空间中不同的直线或平面,对下列四种情形:①x,y,z均为直线;②x,y是直线,z是平面;③x,y是平面,z是直线;④x,y,z均为平面.其中使“x∥z且y∥z?x∥y”为真命题的是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-5不等式选讲 练习卷(解析版) 题型:填空题
已知a,b,m,n均为正数,且a+b=1,mn=2,则(am+bn)·(bm+an)的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-4坐标系与参数方程练习卷(解析版) 题型:选择题
在极坐标系中,圆ρ=2cos θ的垂直于极轴的两条切线方程分别为( )
A.θ=0(ρ∈R)和ρcos θ=2
B.θ=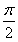 (ρ∈R)和ρcos θ=2
(ρ∈R)和ρcos θ=2
C.θ=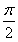 (ρ∈R)和ρcos θ=1
(ρ∈R)和ρcos θ=1
D.θ=0(ρ∈R)和ρcos θ=1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-1几何证明选讲练习卷(解析版) 题型:解答题
如图,已知PE切⊙O于点E,割线PBA交⊙O于A,B两点,∠APE的平分线和AE,BE分别交于点C,D.
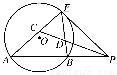
求证:(1)CE=DE;(2)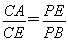 .
.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试解答题保分训练练习卷(解析版) 题型:解答题
设角A,B,C为△ABC的三个内角.
(1)设f(A)=sin A+2sin 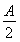 ,当A取A0时,f(A)取极大值f(A0),试求A0和f(A0)的值;
,当A取A0时,f(A)取极大值f(A0),试求A0和f(A0)的值;
(2)当A取A0时, ·
·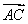 =-1,求BC边长的最小值.
=-1,求BC边长的最小值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试解答题保分训练练习卷(解析版) 题型:解答题
设正项数列{an}的前n项和是Sn,若{an}和{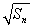 }都是等差数列,且公差相等.
}都是等差数列,且公差相等.
(1)求{an}的通项公式;
(2)若a1, a2,a5恰为等比数列{bn}的前三项,记数列cn=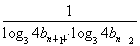 ,数列{cn}的前n项和为Tn,求Tn.
,数列{cn}的前n项和为Tn,求Tn.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(四)第二章第一节练习卷(解析版) 题型:选择题
若函数f(x)= 则f(f(10))=( )
则f(f(10))=( )
(A)lg101 (B)2 (C)1 (D)0
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(五)第二章第二节练习卷(解析版) 题型:选择题
设函数f(x)=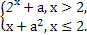 若f(x)的值域为R,则常数a的取值范围是( )
若f(x)的值域为R,则常数a的取值范围是( )
(A)(-∞,-1]∪[2,+∞)
(B)[-1,2]
(C)(-∞,-2]∪[1,+∞)
(D)[-2,1]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com