
【题目】已知三次函数![]() ,
,
(1)若函数![]() 过点
过点![]() 且在点
且在点![]() 处的切线方程是
处的切线方程是![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)在(1)的条件下,若对于区间![]() 上任意两个自变量的值
上任意两个自变量的值![]() ,
,
都有![]() ,求实数
,求实数![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】某景区客栈的工作人员为了控制经营成本,减少浪费,合理安排入住游客的用餐,他们通过统计每个月入住的游客人数,发现每年各个月份来客栈入住的游客人数会发生周期性的变化,并且有以下规律:
①每年相同的月份,入住客栈的游客人数基本相同;
②入住客栈的游客人数在2月份最少,在8月份最多,相差约400人;
③2月份入住客栈的游客约为100人,随后逐月递增直到8月份达到最多.
(1)若入住客栈的游客人数![]() 与月份
与月份![]() 之间的关系可用函数
之间的关系可用函数![]() (
(![]() ,
, ![]() ,
, ![]() )近似描述,求该函数解析式;
)近似描述,求该函数解析式;
(2)请问哪几个月份要准备不少于400人的用餐?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.

根据该折线图,下列结论正确的是( )
A. 月接待游客逐月增加
B. 年接待游客量逐年减少
C. 各年的月接待游客量高峰期大致在7,8月
D. 各年1月至6月的月接待游客相对于7月至12月,波动性更大,变化比较明显
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为圆O的直径,点E,F在圆O上,且AB//EF,AB=2EF,矩形ABCD所在的平面和圆O所在的平面互相垂直.
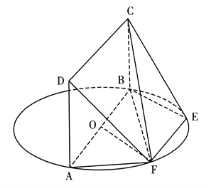
(I)证明:OF//平面BEC;
(Ⅱ)证明:平面ADF![]() 平面BCF.
平面BCF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中,真命题有________.(写出所有真命题的序号)
①若a,b,c∈R,则“ac2>bc2”是“a>b”成立的充分不必要条件;
②命题“x0∈R,x+x0+1<0”的否定是“x∈R,x2+x+1≥0”;
③命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|<2,则-2<x<2”;
④函数f(x)=ln x+x-![]() 在区间(1,2)上有且仅有一个零点.
在区间(1,2)上有且仅有一个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数,给出下列命题:
①若函数f(x)是R上周期为3的偶函数,且满足f(1)=1,则f(2)-f(-4)=0;
②若函数f(x)满足f(x+1)f(x)=2 017,则f(x)是周期函数;
③若函数g(x)=![]() 是偶函数,则f(x)=x+1;
是偶函数,则f(x)=x+1;
④函数y=![]() 的定义域为
的定义域为![]() .
.
其中正确的命题是________.(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,圆![]() 的方程为
的方程为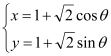 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)当![]() 时,判断直线
时,判断直线![]() 与
与![]() 的关系;
的关系;
(II)当![]() 上有且只有一点到直线
上有且只有一点到直线![]() 的距离等于
的距离等于![]() 时,求
时,求![]() 上到直线
上到直线![]() 距离为
距离为![]() 的点的坐标.
的点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com