
分析 (1)利用生成数列,与控制函数的意义即可得出.
(2)对m分类讨论:可得bm.进而得出前n项和.
(3)依题意:${a_n}={2^n}$,f(1)=A,f(2)=8A,f(5)=125A,设b1=t,即数列{an}中,不超过A的项恰有t项,所以2t≤A<2t+1,同理:2t+d≤8A<2t+d+1,2t+2d≤125A<2t+2d+1,可得d<4,d为正整数,得出d=1,2,3,分类讨论即可得出.
解答 解:(1)m=1,则a1=1≤1,∴b1=1;
m=2,则a1=1<4,a2=4≤4,∴b2=2;
m=3,则a1=1<9,a2=4<9,a3=9≤9,∴b3=3.
(2)m为偶数时,则2n≤m,则${b_m}=\frac{m}{2}$;
m为奇数时,则2n≤m-1,则${b_m}=\frac{m-1}{2}$;
∴${b_m}=\left\{{\begin{array}{l}{\frac{m-1}{2}\;\;\;(m为奇数)}\\{\frac{m}{2}\;\;\;\;\;\;(m为偶数)}\end{array}}\right.$,
m为偶数时,则${S_m}={b_1}+{b_2}+…+{b_m}=\frac{1}{2}(1+2+…+m)-\frac{1}{2}×\frac{m}{2}=\frac{m^2}{4}$;
m为奇数时,则${S_m}={b_1}+{b_2}+…+{b_m}={S_{m+1}}-{b_{m+1}}=\frac{{{{(m+1)}^2}}}{4}-\frac{m+1}{2}=\frac{{{m^2}-1}}{4}$;
∴${S_m}=\left\{{\begin{array}{l}{\frac{{{m^2}-1}}{4}\;\;\;(m为奇数)}\\{\frac{m^2}{4}\;\;\;\;\;\;(m为偶数)}\end{array}}\right.$.
(3)依题意:${a_n}={2^n}$,f(1)=A,f(2)=8A,f(5)=125A,
设b1=t,即数列{an}中,不超过A的项恰有t项,所以2t≤A<2t+1,
同理:2t+d≤8A<2t+d+1,2t+2d≤125A<2t+2d+1,可得:
$\begin{array}{l}{2^t}≤A<{2^{t+1}},\\{2^{t+d-3}}≤A<{2^{t+d-2}},\\ \frac{{{2^{t+2d}}}}{125}≤A<\frac{{{2^{t+2d+1}}}}{125},\end{array}$
故$max\{{2^t},{2^{t+d-3}},\frac{{{2^{t+2d}}}}{125}\}≤A<min\{{2^{t+1}},{2^{t+d-2}},\frac{{{2^{t+2d+1}}}}{125}\}$,
由以下关系:
$\begin{array}{l}{2^{t+d-3}}<{2^{t+1}},\\ \frac{{{2^{t+2d}}}}{125}<{2^{t+d-2}},\end{array}$
得d<4,
∵d为正整数,∴d=1,2,3.
当d=1时,$max\{{2^t},{2^{t+d-3}},\frac{{{2^{t+2d}}}}{125}\}=max\{{2^t},\frac{2^t}{4},\frac{{4×{2^t}}}{125}\}={2^t}$,
$min\{{2^{t+1}},{2^{t+d-2}},\frac{{{2^{t+2d+1}}}}{125}\}=min\{{2^{t+1}},\frac{2^t}{2},\frac{{8×{2^t}}}{125}\}=\frac{{8×{2^t}}}{125}<{2^t}$不合题意,舍去;
当d=2时,$max\{{2^t},{2^{t+d-3}},\frac{{{2^{t+2d}}}}{125}\}=max\{{2^t},{2^{t-1}},\frac{{16×{2^t}}}{125}\}={2^t}$,
$min\{{2^{t+1}},{2^{t+d-2}},\frac{{{2^{t+2d+1}}}}{125}\}=min\{{2^{t+1}},{2^t},\frac{{32×{2^t}}}{125}\}=\frac{{32×{2^t}}}{125}<{2^t}$不合题意,舍去;
当d=3时,$max\{{2^t},{2^{t+d-3}},\frac{{{2^{t+2d}}}}{125}\}=max\{{2^t},{2^t},\frac{{64×{2^t}}}{125}\}={2^t}$,
$min\{{2^{t+1}},{2^{t+d-2}},\frac{{{2^{t+2d+1}}}}{125}\}=min\{{2^{t+1}},{2^{t+1}},\frac{{128×{2^t}}}{125}\}=\frac{{128×{2^t}}}{125}>{2^t}$,适合题意.
此时${2^t}≤A<\frac{128}{125}×{2^t}$,b1=t,b2=t+3,b5=t+6,∴t+3≤b3≤t+6.
∵b3=10,∴4≤t≤7,
∵t为整数,∴t=4,t=5,t=6或t=7.
∵f(3)=27A,b3=10,
∴210≤27A<211,∴$\frac{{{2^{10}}}}{27}≤A<\frac{{{2^{11}}}}{27}$.
当t=4时,${2^4}≤A<\frac{{{2^{11}}}}{125}$,∴无解.
当t=5时,${2^5}≤A<\frac{{{2^{12}}}}{125}$,∴无解.
当t=6时,${2^6}≤A<\frac{{{2^{13}}}}{125}$,∴$64≤A<\frac{{{2^{13}}}}{125}$.
当t=7时,${2^7}≤A<\frac{{{2^{14}}}}{125}$,∴无解,∴${2^6}≤A<\frac{{{2^{13}}}}{125}$.
∵A∈N*,∴A=64或A=65.
综上:d=3,A=64或65.
点评 本题考查了递推关系、数列的通项公式、等比数列的通项公式、分类讨论方法,考查了推理能力与计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
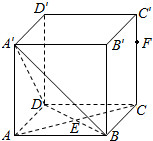 如图,正方体ABCD-A′B′C′D′中,$\overrightarrow{BD}=2\overrightarrow{BE}$.设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )
如图,正方体ABCD-A′B′C′D′中,$\overrightarrow{BD}=2\overrightarrow{BE}$.设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )| A. | $[\frac{{\sqrt{3}}}{3},1]$ | B. | $[\frac{{2\sqrt{2}}}{3},1]$ | C. | $[\frac{{\sqrt{6}}}{3},\frac{{2\sqrt{2}}}{3}]$ | D. | $[\frac{{\sqrt{6}}}{3},1]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
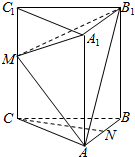 如图,在正三棱柱ABC-A1B1C1(侧棱垂直于底面,且底面是正三角形)中,AC=CC1=6,M是棱CC1上一点.
如图,在正三棱柱ABC-A1B1C1(侧棱垂直于底面,且底面是正三角形)中,AC=CC1=6,M是棱CC1上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7π}{6}$ | B. | $\frac{5π}{4}$ | C. | $\frac{4π}{3}$ | D. | $\frac{5π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2-2$\sqrt{2}$,2+2$\sqrt{2}$] | B. | [2-2$\sqrt{2}$,1-$\sqrt{3}$] | ||
| C. | [1+$\sqrt{3}$,2+2$\sqrt{2}$] | D. | [2-2$\sqrt{2}$,1-$\sqrt{3}$]∪[1+$\sqrt{3}$,2+2$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com