【题目】已知数列{an}是公比不为1的等比数列，a1=1，且a1 ， a3 ， a2成等差数列．
（1）求数列{an}的通项；
（2）若数列{an}的前n项和为Sn ， 试求Sn的最大值．
【答案】
（1）解：设等比数列的公比为q，
∵a1，a3，a2成等差数列，
∴2a3=a1+a2，又a1=1，
∴2×1×q2=1+1×q，解得q=﹣ 
，或q=1（舍）．
∴ 
．
（2）解：由等比数列求和得，Sn=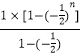 
= 
，
当n为奇数时， 
=1；
当n为偶数时， 
．
∴Sn的最大值为1．
【解析】（1）设等比数列的公比为q，由a1 ， a3 ， a2成等差数列，得2a3=a1+a2 ， 由通项公式可得q的方程，从而可求q，通项an；（2）由等比数列求和公式可得Sn ， 分n为奇数、偶数可得Sn的范围，从而可得结果；
【考点精析】利用数列的前n项和和等差数列的性质对题目进行判断即可得到答案，需要熟知数列{an}的前n项和sn与通项an的关系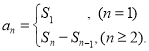
；在等差数列{an}中，从第2项起，每一项是它相邻二项的等差中项；相隔等距离的项组成的数列是等差数列．
智趣寒假作业云南科技出版社系列答案科目：高中数学 来源： 题型：
【题目】已知二次函数f（x）=x2+bx+c（其中b，c为实常数）．
（1）若b＞2，且y=f（sinx）（x∈R）的最大值为5，最小值为﹣1，求函数y=f（x）的解析式；
（2）是否存在这样的函数y=f（x），使得{y|y=x2+bx+c，﹣1≤x≤0}=[﹣1，0]，若存在，求出函数y=f（x）的解析式；若不存在，请说明理由．
（3）记集合A={x|f（x）=x，x∈R}，B={x|f（f（x））=x，x∈R}．
①若A≠，求证：B≠；
②若A=，判断B是否也为空集．
查看答案和解析>>
科目：高中数学 来源： 题型：
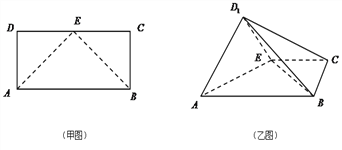
【题目】【2017四川宜宾二诊】如甲图所示，在矩形
中， 
， 
， 
是
的中点，将
沿
折起到
位置，使平面
平面
，得到乙图所示的四棱锥
．
（Ⅰ）求证： 
平面
；
（Ⅱ）求二面角
的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】《中国谜语大会》是中央电视台科教频道的一档集文化、益智、娱乐为一体的大型电视竞猜节目，目的是为弘扬中国传统文化、丰富群众文化生活．为选拔选手参加“中国谜语大会”，某地区举行了一次“谜语大赛”活动．为了了解本次竞赛选手的成绩情况，从中抽取了部分选手的分数（得分取正整数，满分为100分）作为样本进行统计．按照[50，60），[60，70），[70，80），[80，90），[90，100）的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出得分在[50，60），[90，100）的数据）．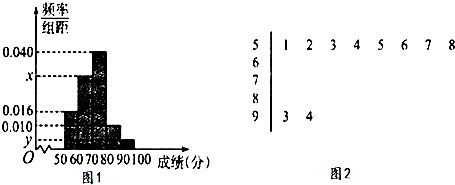 
（1）求样本容量n和频率分布直方图中的x，y的值；
（2）分数在[80，90）的学生中，男生有2人，现从该组抽取三人“座谈”，求至少有两名女生的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆C经过点A（1，3）、B（2，2），并且直线m：3x﹣2y=0平分圆C．
（1）求圆C的方程；
（2）若过点D（0，1），且斜率为k的直线l与圆C有两个不同的交点M、N．
（Ⅰ）求实数k的取值范围；
（Ⅱ）若 
=12，求k的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的长势情况，从两块地各随机抽取了10株树苗，分别测出它们的高度如下（单位：cm）
甲：19 20 21 23 25 29 32 33 37 41
乙：10 24 26 30 34 37 44 46 47 48
（1）用茎叶图表示上述两组数据，并对两块地抽取树苗的高度进行比较，写出一个统计结论；
（2）苗圃基地分配这20株树苗的栽种任务，小王在苗高大于40cm的5株树苗中随机的选种2株，则小王没有选到甲苗圃树苗的概率是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知A（x1 ， y1），B（x2 ， y2）是函数f（x）=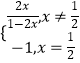 
的图象上的任意两点（可以重合），点M在直线x= 
上，且 
= 
．
（1）求x1+x2的值及y1+y2的值；
（2）已知S1=0，当n≥2时，Sn=f（ 
）+f（ 
）+f（ 
）+…+f（ 
），求Sn ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
