
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,且2cosAcosC(tanAtanC﹣1)=1.
(Ⅰ)求B的大小;
(Ⅱ)若 ![]() ,
, ![]() ,求△ABC的面积.
,求△ABC的面积.
【答案】解:(Ⅰ)由2cosAcosC(tanAtanC﹣1)=1得:2cosAcosC( ![]() ﹣1)=1, ∴2(sinAsinC﹣cosAcosC)=1,即cos(A+C)=﹣
﹣1)=1, ∴2(sinAsinC﹣cosAcosC)=1,即cos(A+C)=﹣ ![]() ,
,
∴cosB=﹣cos(A+C)= ![]() ,
,
又0<B<π,
∴B= ![]() ;
;
(Ⅱ)由余弦定理得:cosB= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
又a+c= ![]() ,b=
,b= ![]() ,
,
∴ ![]() ﹣2ac﹣3=ac,即ac=
﹣2ac﹣3=ac,即ac= ![]() ,
,
∴S△ABC= ![]() acsinB=
acsinB= ![]() ×
× ![]() ×
× ![]() =
= ![]()
【解析】(Ⅰ)已知等式括号中利用同角三角函数间基本关系切化弦,去括号后利用两角和与差的余弦函数公式化简,再由诱导公式变形求出cosB的值,即可确定出B的大小;(Ⅱ)由cosB,b的值,利用余弦定理列出关系式,再利用完全平方公式变形,将a+b以及b的值代入求出ac的值,再由cosB的值,利用三角形面积公式即可求出三角形ABC面积.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期是π,若其图象向右平移
)的最小正周期是π,若其图象向右平移 ![]() 个单位后得到的函数为奇函数,则函数y=f(x)的图象( )
个单位后得到的函数为奇函数,则函数y=f(x)的图象( )
A.关于点( ![]() ,0)对称
,0)对称
B.关于直线x= ![]() 对称
对称
C.关于点( ![]() ,0)对称
,0)对称
D.关于直线x= ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商丘市大型购物中心——万达广场将于2018年7月6日全面开业,目前正处于试营业阶段,某按摩椅经销商为调查顾客体验按摩椅的时间,随机调查了50名顾客,体验时间(单位:分钟)落在各个小组的频数分布如下表:
体验 时间 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
(1)求这![]() 名顾客体验时间的样本平均数
名顾客体验时间的样本平均数![]() ,中位数
,中位数![]() ,众数
,众数![]() ;
;
(2)已知体验时间为![]() 的顾客中有2名男性,体验时间为
的顾客中有2名男性,体验时间为![]() 的顾客中有3名男性,为进一步了解顾客对按摩椅的评价,现随机从体验时间为
的顾客中有3名男性,为进一步了解顾客对按摩椅的评价,现随机从体验时间为![]() 和
和![]() 的顾客中各抽一人进行采访,求恰抽到一名男性的概率.
的顾客中各抽一人进行采访,求恰抽到一名男性的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】鹰潭市龙虎山花语世界位于中国第八处世界自然遗产,世界地质公元、国家自然文化双遗产地、国家AAAAA级旅游景区﹣﹣龙虎山主景区排衙峰下,是一座独具现代园艺风格的花卉公园,园内汇集了3000余种花卉苗木,一年四季姹紫嫣红花香四溢.花园景观融合法、英、意、美、日、中六大经典园林风格,景观设计唯美新颖.玫瑰花园、香草花溪、台地花海、植物迷宫、儿童乐园等景点错落有致,交相呼应又自成一体,是世界园艺景观的大展示.该景区自2015年春建成试运行以来,每天游人如织,郁金香、向日葵、虞美人等赏花旺季日入园人数最高达万人.某学校社团为了解进园旅客的具体情形以及采集旅客对园区的建议,特别在2017年4月1日赏花旺季对进园游客进行取样调查,从当日12000名游客中抽取100人进行统计分析,结果如下:(表一)
年龄 | 频数 | 频率 | 男 | 女 |
[0,10) | 10 | 0.1 | 5 | 5 |
[10,20) | ① | ② | ③ | ④ |
[20,30) | 25 | 0.25 | 12 | 13 |
[30,40) | 20 | 0.2 | 10 | 10 |
[40,50) | 10 | 0.1 | 6 | 4 |
[50,60) | 10 | 0.1 | 3 | 7 |
[60,70) | 5 | 0.05 | 1 | 4 |
[70,80) | 3 | 0.03 | 1 | 2 |
[80,90) | 2 | 0.02 | 0 | 2 |
合计 | 100 | 1.00 | 45 | 55 |
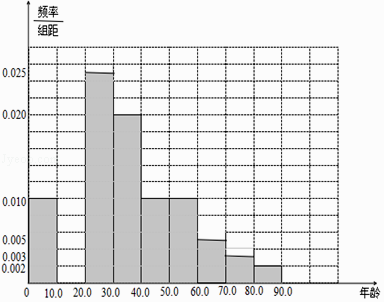
(1)完成表格一中的空位①﹣④,并在答题卡中补全频率分布直方图,并估计2017年4月1日当日接待游客中30岁以下人数.
(2)完成表格二,并问你能否有97.5%的把握认为在观花游客中“年龄达到50岁以上”与“性别”相关?
50岁以上 | 50岁以下 | 合计 | |
男生 | |||
女生 | |||
合计 |
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:k2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
(3)按分层抽样(分50岁以上与50以下两层)抽取被调查的100位游客中的10人作为幸运游客免费领取龙虎山内部景区门票,再从这10人中选取2人接受电视台采访,设这2人中年龄在50岁以上(含)的人数为ξ,求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图. 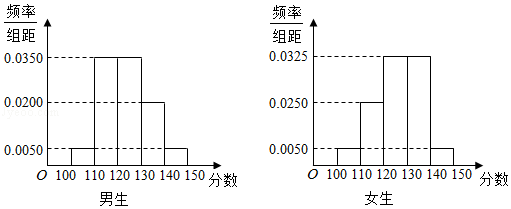
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
附:K2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2022年北京冬季奥运会, 某校开设了冰球选修课,12名学生被分成甲、乙两组进行训练.他们的身高(单位:cm)如下图所示:
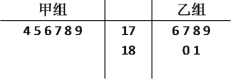
设两组队员身高平均数依次为![]() ,
,![]() ,方差依次为
,方差依次为![]() ,
,![]() ,则下列关系式中完全正确的是( )
,则下列关系式中完全正确的是( )
A. ![]() =
=![]() ,
, ![]() =
=![]() B.
B. ![]() <
<![]() ,
,![]() >
>![]()
C. ![]() <
<![]() ,
,![]() =
=![]() D.
D. ![]() <
<![]() ,
,![]() <
<![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com