
【题目】设等比数列![]() 的公比为
的公比为![]() ,其前
,其前![]() 项和为
项和为![]() ,前
,前![]() 项之积为
项之积为![]() ,并且满足条件:
,并且满足条件:![]() ,
,![]() ,
,![]() ,下列结论中正确的是( )
,下列结论中正确的是( )
A. ![]() B.
B. ![]()
C. ![]() 是数列
是数列![]() 中的最大值 D. 数列
中的最大值 D. 数列![]() 无最小值
无最小值
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
【题目】设等比数列![]() 的公比为
的公比为![]() ,其前
,其前![]() 项和为
项和为![]() ,前
,前![]() 项之积为
项之积为![]() ,并且满足条件:
,并且满足条件:![]() ,
,![]() ,
,![]() ,下列结论中正确的是( )
,下列结论中正确的是( )
A. ![]() B.
B. ![]()
C. ![]() 是数列
是数列![]() 中的最大值 D. 数列
中的最大值 D. 数列![]() 无最小值
无最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了改善居民的休闲娱乐活动场所,现有一块矩形![]() 草坪如下图所示,已知:
草坪如下图所示,已知:![]() 米,
米,![]() 米,拟在这块草坪内铺设三条小路
米,拟在这块草坪内铺设三条小路![]() 、
、![]() 和
和![]() ,要求点
,要求点![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 时上,且
时上,且![]() .
.
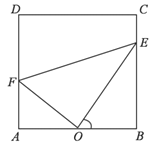
(1)设![]() ,试求
,试求![]() 的周长
的周长![]() 关于
关于![]() 的函数解析式,并求出此函数的定义域;
的函数解析式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为![]() 元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点
的中点
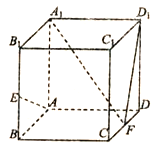
(1)求证:![]() 面
面![]() ;
;
(2)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 面
面![]() ,若存在,试确定
,若存在,试确定![]() 的值,若不存在说明理由;
的值,若不存在说明理由;
(3)在(2)的条件下,求面![]() 与面
与面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为进一步贯彻落实“十九”大精神,某高校组织了“歌颂祖国,紧跟党走”为主题的党史知识竞赛,从参加竞赛的学生中,随机抽取40名学生,将其成绩分为六段![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
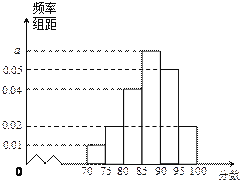
(1)求图中![]() 的值;
的值;
(2)若从竞赛成绩在![]() 与
与![]() 两个分数段的学生
两个分数段的学生![]() 中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于
中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于![]() 分为事件
分为事件![]() ,求事件发生的概率.
,求事件发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com