
如图,摄影爱好者在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为30°,已知摄影爱好者的身高约为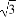 米(将眼睛S距地面的距离SA按
米(将眼睛S距地面的距离SA按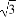 米处理).
米处理).
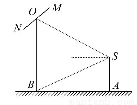
(1)求摄影爱好者到立柱的水平距离AB和立柱的高度OB.
(2)立柱的顶端有一长为2米的彩杆MN,且MN绕其中点O在摄影爱好者与立柱所在的平面内旋转.在彩杆转动的任意时刻,摄影爱好者观察彩杆MN的视角∠MSN(设为θ)是否存在最大值?若存在,请求出∠MSN取最大值时cosθ的值;若不存在,请说明理由.
(1) AB为3米 OB为2 米 (2) 当视角∠MSN取最大值时,cosθ=
米 (2) 当视角∠MSN取最大值时,cosθ=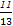 .
.
【解析】(1)如图,作SC⊥OB于C,
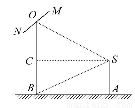
依题意∠CSB=30°,∠ASB=60°.
又SA= ,故在Rt△SAB中,可求得AB=
,故在Rt△SAB中,可求得AB=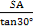 =3,
=3,
即摄影爱好者到立柱的水平距离AB为3米.
在Rt△SCO中,SC=3,∠CSO=30°,OC=SC·tan 30°= ,
,
又BC=SA= ,故OB=2
,故OB=2 ,即立柱的高度OB为2
,即立柱的高度OB为2 米.
米.
(2)方法一:如图,以O为原点,以水平方向向右为x轴正方向建立平面直角坐标系,连接SM,SN,
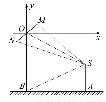
设M(cosα,sinα),α∈[0,2π),
则N(-cosα,-sinα),由(1)知S(3,- ).
).
故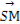 =(cosα-3,sinα+
=(cosα-3,sinα+ ),
),
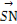 =(-cosα-3,-sinα+
=(-cosα-3,-sinα+ ),
),
∵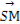 ·
·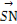 =(cosα-3)·(-cosα-3)+(sinα+
=(cosα-3)·(-cosα-3)+(sinα+ )·(-sinα+
)·(-sinα+ )=11.
)=11.
|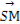 |·|
|·|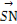 |=
|= ·
·
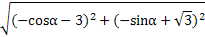
=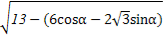 ·
·

=
=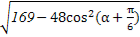 .
.
由α∈[0,2π)知|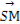 |·|
|·|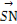 |∈[11,13].
|∈[11,13].
所以cos∠MSN=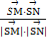 ∈[
∈[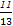 ,1],易知∠MSN为锐角,
,1],易知∠MSN为锐角,
故当视角∠MSN取最大值时,cosθ=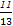 .
.
方法二:∵cos∠MOS=-cos∠NOS,
∴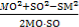 =-
=-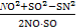
于是得SM2+SN2=26从而
cosθ=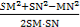 ≥
≥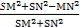 =
=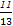 .
.
又∠MSN为锐角,
故当视角∠MSN取最大值时,cosθ=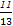 .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十九第八章第十节练习卷(解析版) 题型:解答题
已知椭圆E: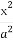 +
+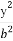 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=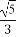 ,a2与b2的等差中项为
,a2与b2的等差中项为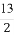 .
.
(1)求椭圆E的方程.
(2)A,B是椭圆E上的两点,线段AB的垂直平分线与x轴相交于点P(t,0),求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十一第八章第二节练习卷(解析版) 题型:解答题
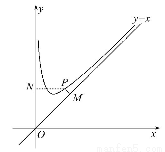
如图,函数f(x)=x+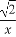 的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.
的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.
(1)证明:|PM|·|PN|为定值.
(2)O为坐标原点,求四边形OMPN面积的最小值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十第三章第四节练习卷(解析版) 题型:解答题
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<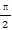 ,x∈R)的图象的一部分如图所示.
,x∈R)的图象的一部分如图所示.
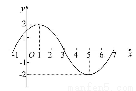
(1)求函数f(x)的解析式.
(2)当x∈[-6,- ]时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.
]时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十第三章第四节练习卷(解析版) 题型:选择题
已知函数f(x)= sin(2x+
sin(2x+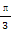 ),其中x∈R,则下列结论中正确的是( )
),其中x∈R,则下列结论中正确的是( )
(A)f(x)是最小正周期为π的偶函数
(B)f(x)的一条对称轴是x=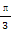
(C)f(x)的最大值为2
(D)将函数y= sin2x的图象左移
sin2x的图象左移 个单位得到函数f(x)的图象
个单位得到函数f(x)的图象
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十四第三章第八节练习卷(解析版) 题型:选择题
线段AB外有一点C,∠ABC=60°,AB=200km,汽车以80km/h的速度由A向B行驶,同时摩托车以50km/h的速度由B向C行驶,则运动开始几小时后,两车的距离最小( )
(A)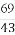 (B)1 (C)
(B)1 (C)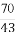 (D)2
(D)2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十八第四章第四节练习卷(解析版) 题型:解答题
已知M(1+cos 2x,1),N(1,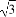 sin2x+a)(x∈R,a∈R,a是常数),且y=
sin2x+a)(x∈R,a∈R,a是常数),且y= ·
· (O为坐标原点).
(O为坐标原点).
(1)求y关于x的函数关系式y=f(x).
(2)若x∈[0,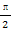 ]时,f(x)的最大值为2013,求a的值.
]时,f(x)的最大值为2013,求a的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十二第三章第六节练习卷(解析版) 题型:选择题
若函数f(x)=(sinx+cosx)2-2cos2x-m在[0,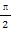 ]上有零点,则实数m的取值范围为( )
]上有零点,则实数m的取值范围为( )
(A)[-1,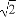 ] (B)[-1,1]
] (B)[-1,1]
(C)[1,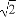 ] (D)[-
] (D)[-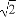 ,-1]
,-1]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com