
【题目】已知向量![]() =(cosx,sinx),
=(cosx,sinx),![]() =(cosx,﹣sinx),函数
=(cosx,﹣sinx),函数![]() .
.
(1)若![]() ,x
,x![]() (0,
(0,![]() ),求tan(x+
),求tan(x+![]() )的值;
)的值;
(2)若![]() ,
,![]() (
(![]() ,
,![]() ),
),![]() ,
,![]() (0,
(0,![]() ),求
),求![]() 的值.
的值.
【答案】(1)-2-![]() ;(2)
;(2)![]()
【解析】
(1)由向量![]() =(cosx,sinx),
=(cosx,sinx),![]() =(cosx,-sinx),利用数量积运算得到f(x)=cos2x+
=(cosx,-sinx),利用数量积运算得到f(x)=cos2x+![]() ,根据f(
,根据f(![]() )=1,求得cosx=
)=1,求得cosx=![]() ,得到x=
,得到x=![]() ,然后利用两角和的正切公式求解.
,然后利用两角和的正切公式求解.
(2)由f(α)=-![]() ,得到cos2α=-
,得到cos2α=-![]() ,进而得到sin2α=-
,进而得到sin2α=-![]() ,再由sinβ=
,再由sinβ=![]() ,得到 cosβ=
,得到 cosβ=![]() , 然后利用两角和的余弦公式求解.
, 然后利用两角和的余弦公式求解.
(1)因为向量![]() =(cosx,sinx),
=(cosx,sinx),![]() =(cosx,-sinx),
=(cosx,-sinx),
所以f(x)=![]() ·
·![]() +
+![]() =cos2x-sin2x+
=cos2x-sin2x+![]() =cos2x+
=cos2x+![]() .
.
因为f(![]() )=1,
)=1,
所以cosx+![]() =1,
=1,
即cosx=![]() .
.
又因为x∈(0,π) ,
所以x=![]() ,
,
所以tan(x+![]() )=tan(
)=tan(![]() +
+![]() )=
)=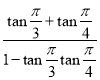 =-2-
=-2-![]() .
.
(2)若f(α)=-![]() ,则cos2α+
,则cos2α+![]() =-
=-![]() ,即cos2α=-
,即cos2α=-![]() .
.
因为α∈(![]() ,
,![]() ),
),
所以2α∈(π,![]() ),
),
所以sin2α=-![]() =-
=-![]() .
.
因为sinβ=![]() ,β∈(0,
,β∈(0,![]() ),
),
所以cosβ=![]() =
=![]() ,
,
所以cos(2α+β)=cos2αcosβ-sin2αsinβ=(-![]() )×
)×![]() -(-
-(-![]() )×
)×![]() =
=![]() .
.
又因为2α∈(π,![]() ),β∈(0,
),β∈(0,![]() ),
),
所以2α+β∈(π,2π),
所以2α+β的值为![]() .
.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】2019新型冠状病毒感染的肺炎的传播有飞沫、气溶胶、接触等途径,为了有效抗击疫情,隔离性防护是一项具体有效措施.某市为有效防护疫情,宣传居民尽可能不外出,鼓励居民的生活必需品可在网上下单,商品由快递业务公司统一配送(配送费由政府补贴).快递业务主要由甲公司与乙公司两家快递公司承接:“快递员”的工资是“底薪+送件提成”.这两家公司对“快递员”的日工资方案为:甲公司规定快递员每天底薪为70元,每送件一次提成1元;乙公司规定快递员每天底薪为120元,每日前83件没有提成,超过83件部分每件提成5元,假设同一公司的快递员每天送件数相同,现从这两家公司往年忙季各随机抽取一名快递员并调取其100天的送件数,得到如下条形图:

(1)求乙公司的快递员一日工资y(单位:元)与送件数n的函数关系;
(2)若将频率视为概率,回答下列问题:
①记甲公司的“快递员”日工资为X(单位:元).求X的分布列和数学期望;
②小王想到这两家公司中的一家应聘“快递员”的工作,如果仅从日收入的角度考虑,请你利用所学过的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ∥
∥![]() ,
,![]() ,
,![]() 是等边三角形,侧面
是等边三角形,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是棱
是棱![]() 上靠近点
上靠近点![]() 的一个三等分点.
的一个三等分点.

(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)设点![]() 是线段
是线段![]() (含端点)上的动点,若直线
(含端点)上的动点,若直线![]() 与底面
与底面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | 不大于2000元 | 大于2000元 |
仅使用A | 27人 | 3人 |
仅使用B | 24人 | 1人 |
(Ⅰ)估计该校学生中上个月A,B两种支付方式都使用的人数;
(Ⅱ)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于2000元的概率;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现他本月的支付金额大于2000元.结合(Ⅱ)的结果,能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱中ABC—A1B1C1,ABAC,AB=3,AC=4,B1CAC1.

(1)求AA1的长;
(2)试判断在侧棱BB1上是否存在点P,使得直线PC与平面AA1C1C所成角和二面角B—A1C—A的大小相等,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图(如图①)、90后从事互联网行业岗位分布条形图(如图②),则下列结论中不一定正确的是( )


注:90后指1990年及以后出生,80后指1980~1989年之间出生,80前指1979年及以前出生.
A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图已知![]() ,
,![]() ,
,![]() 、
、![]() 分別为
分別为![]() 、
、![]() 的中点
的中点![]() ,将
,将![]() 沿
沿![]() 折起,得到四棱锥
折起,得到四棱锥![]() ,
,![]() 为
为![]() 的中点.
的中点.
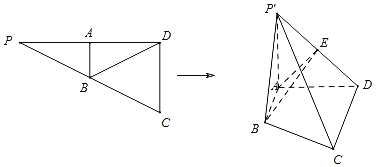
(1)证明:![]() 平面
平面![]() ;
;
(2)当正视图方向与向量![]() 的方向相同时,
的方向相同时,![]() 的正视图为直角三角形,求此时二面角
的正视图为直角三角形,求此时二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com