
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,若
时,若![]() 在
在![]() 上有零点,求实数
上有零点,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析(Ⅱ)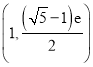
【解析】试题分析:(Ⅰ) ![]() ,结合定义域讨论导数的正负求单调区间即可;
,结合定义域讨论导数的正负求单调区间即可;
(Ⅱ)当![]() 时,
时, ![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .所以
.所以![]() 在
在![]() 上有零点的必要条件是
上有零点的必要条件是![]() ,得
,得![]() ,讨论
,讨论![]() 和
和![]() 时函数单调性求解参数范围即可.
时函数单调性求解参数范围即可.
试题解析:
解:(Ⅰ)函数![]() 的定义域为
的定义域为![]() ,
,
![]() .
.
由![]() 得
得![]() 或
或![]() .
.
当![]() 时,
时, ![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 的单调递减区间是
的单调递减区间是![]() ,没有单调递增区间.
,没有单调递增区间.
当![]() 时,
时, ![]() 的变化情况如下表:
的变化情况如下表:
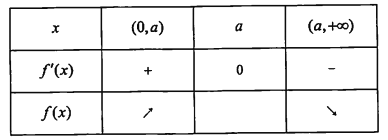
所以![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
当![]() 时,
时, ![]() 的变化情况如下表:
的变化情况如下表:
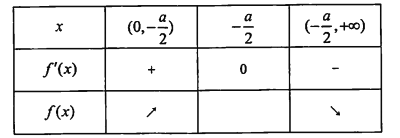
所以![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
(Ⅱ)当![]() 时,
时, ![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
所以![]() 在
在![]() 上有零点的必要条件是
上有零点的必要条件是![]() ,
,
即![]() ,所以
,所以![]() .
.
而![]() ,所以
,所以![]() .
.
若![]() ,
, ![]() 在
在![]() 上是减函数,
上是减函数, ![]() ,
, ![]() 在
在![]() 上没有零点.
上没有零点.
若![]() ,
, ![]() ,
, ![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
所以![]() 在
在![]() 上有零点等价于
上有零点等价于![]() ,
,
即![]() ,解得
,解得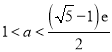 .
.
综上所述,实数![]() 的取值范围是
的取值范围是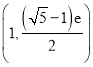 .
.


科目:高中数学 来源: 题型:
【题目】某大型娱乐场有两种型号的水上摩托,管理人员为了了解水上摩托的使用及给娱乐城带来的经济收入情况,对该场所最近6年水上摩托的使用情况进行了统计,得到相关数据如表:
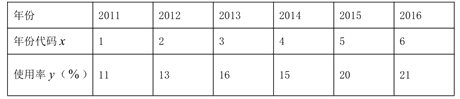
(1)请根据以上数据,用最小二乘法求水上摩托使用率![]() 关于年份代码
关于年份代码![]() 的线性回归方程,并预测该娱乐场2018年水上摩托的使用率;
的线性回归方程,并预测该娱乐场2018年水上摩托的使用率;
(2)随着生活水平的提高,外出旅游的老百姓越来越多,该娱乐场根据自身的发展需要,准备重新购进一批水上摩托,其型号主要是目前使用的Ⅰ型、Ⅱ型两种,每辆价格分别为1万元、1.2万元.根据以往经验,每辆水上摩托的使用年限不超过四年.娱乐场管理部对已经淘汰的两款水上摩托的使用情况分别抽取了50辆进行统计,使用年限如条形图所示:

已知每辆水上摩托从购入到淘汰平均年收益是0.8万元,若用频率作为概率,以每辆水上摩托纯利润(纯利润=收益-购车成本)的期望值为参考值,则该娱乐场的负责人应该选购Ⅰ型水上摩托还是Ⅱ型水上摩托?
附:回归直线方程为![]() ,其中
,其中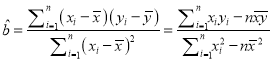 ,
, ![]() .参考数据
.参考数据![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)若函数![]() 在区间
在区间![]() 上是单调函数,试求实数
上是单调函数,试求实数![]() 的取值范围;
的取值范围;
(2)已知函数![]() ,且
,且![]() ,若函数
,若函数![]() 在区间
在区间![]() 上恰有3个零点,求实数
上恰有3个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex-e-x(x∈R,且e为自然对数的底数).
(1)判断函数f(x)的单调性与奇偶性;
(2)是否存在实数t,使不等式f(x-t)+f(x2-t2)≥0对一切x∈R都成立?若存在,求出t;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年4月1日,新华通讯社发布:国务院决定设立河北雄安新区.消息一出,河北省雄县、容城、安新3县及周边部分区域迅速成为海内外高度关注的焦点.
(1)为了响应国家号召,北京市某高校立即在所属的8个学院的教职员工中作了“是否愿意将学校整体搬迁至雄安新区”的问卷调查,8个学院的调查人数及统计数据如下:
调查人数( | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
愿意整体搬迁人数( | 8 | 17 | 25 | 31 | 39 | 47 | 55 | 66 |
请根据上表提供的数据,用最小二乘法求出变量![]() 关于变量
关于变量![]() 的线性回归方程
的线性回归方程![]() 保留小数点后两位有效数字);若该校共有教职员工2500人,请预测该校愿意将学校整体搬迁至雄安新区的人数;
保留小数点后两位有效数字);若该校共有教职员工2500人,请预测该校愿意将学校整体搬迁至雄安新区的人数;
(2)若该校的8位院长中有5位院长愿意将学校整体搬迁至雄安新区,现该校拟在这8位院长中随机选取4位院长组成考察团赴雄安新区进行实地考察,记![]() 为考察团中愿意将学校整体搬迁至雄安新区的院长人数,求
为考察团中愿意将学校整体搬迁至雄安新区的院长人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式及数据:  .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com