
【题目】如图,P是圆x2+y2=4上的动点,P点在x轴上的射影是D,点M满足![]() .
.

(Ⅰ)求动点M的轨迹C的方程
(Ⅱ)设A、B是轨迹C上的不同两点,点E(﹣4,0),且满足![]() ,若λ∈[
,若λ∈[![]() ,1),求直线AB的斜率k的取值范围.
,1),求直线AB的斜率k的取值范围.
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦点分别为
,焦点分别为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上的点,
上的点,![]() 面积的最大值是
面积的最大值是![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上的点,
上的点,![]() 是坐标原点,若
是坐标原点,若![]() 判定四边形
判定四边形![]() 的面积是否为定值?若为定值,求出定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,来自“一带一路”沿线的20国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购.其中共享单车既响应绿色出行号召,节能减排,保护环境,又方便人们短距离出行,增强灵活性.某城市试投放3个品牌的共享单车分别为红车、黄车、蓝车,三种车的计费标准均为每15分钟(不足15分钟按15分钟计)1元,按每日累计时长结算费用,例如某人某日共使用了24分钟,系统计时为30分钟.A同学统计了他1个月(按30天计)每天使用共享单车的时长如茎叶图所示,不考虑每月自然因素和社会因素的影响,用频率近似代替概率.设A同学每天消费![]() 元.
元.
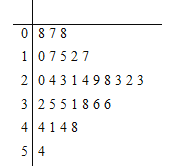
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)各品牌为推广用户使用,推出APP注册会员的优惠活动:红车月功能使用费8元,每天消费打5折;黄车月功能使用费20元,每天前15分钟免费,之后消费打8折;蓝车月功能使用费45元,每月使用22小时之内免费,超出部分按每15分钟1元计费.设![]() 分别为红车,黄车,蓝车的月消费,写出
分别为红车,黄车,蓝车的月消费,写出![]() 与
与![]() 的函数关系式,参考(1)的结果,A同学下个月选择其中一个注册会员,他选哪个费用最低?
的函数关系式,参考(1)的结果,A同学下个月选择其中一个注册会员,他选哪个费用最低?
(3)该城市计划3个品牌的共享单车共3000辆正式投入使用,为节约居民开支,随机调查了100名用户一周的平均使用时长如下表:
时长 | (0,15] | (15,30] | (30,45] | (45,60] |
人数 | 16 | 45 | 34 | 5 |
在(2)的活动条件下,每个品牌各应该投放多少辆?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汉中市2019年油菜花节在汉台区举办,组委会将甲、乙等6名工作人员分配到两个不同的接待处负责参与接待工作,每个接待处至少2人,则甲、乙两人不在同一接待处的分配方法共有( )
A. 12种B. 22种C. 28种D. 30种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有![]() 名学生排成一排,求分别满足下列条件的排法种数,要求列式并给出计算结果.
名学生排成一排,求分别满足下列条件的排法种数,要求列式并给出计算结果.
(1)甲不在两端;
(2)甲、乙相邻;
(3)甲、乙、丙三人两两不得相邻;
(4)甲不在排头,乙不在排尾。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)集合![]() ,
,![]() 或
或![]() ,对于任意
,对于任意![]() ,定义
,定义![]() ,对任意
,对任意![]() ,定义
,定义![]() ,记
,记![]() 为集合
为集合![]() 的元素个数,求
的元素个数,求![]() 的值;
的值;
(2)在等差数列![]() 和等比数列
和等比数列![]() 中,
中,![]() ,
,![]() ,是否存在正整数
,是否存在正整数![]() ,使得数列
,使得数列![]() 的所有项都在数列
的所有项都在数列![]() 中,若存在,求出所有的
中,若存在,求出所有的![]() ,若不存在,说明理由;
,若不存在,说明理由;
(3)已知当![]() 时,有
时,有![]() ,根据此信息,若对任意
,根据此信息,若对任意![]() ,都有
,都有![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,设直线
,设直线![]() 分别是曲线
分别是曲线![]() 的两条不同的切线;
的两条不同的切线;
(1)若函数![]() 为奇函数,且当
为奇函数,且当![]() 时,
时,![]() 有极小值为-4;
有极小值为-4;
(i)求![]() 的值;
的值;
(ii)若直线![]() 亦与曲线
亦与曲线![]() 相切,且三条不同的直线
相切,且三条不同的直线![]() 交于点
交于点![]() ,求实数m的取值范围;
,求实数m的取值范围;
(2)若直线![]() ,直线
,直线![]() 与曲线
与曲线![]() 切于点B且交曲线
切于点B且交曲线![]() 于点D,直线
于点D,直线![]() 与曲线
与曲线![]() 切于点C且交曲线
切于点C且交曲线![]() 于点A,记点
于点A,记点![]() 的横坐标分别为
的横坐标分别为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网站用“100分制”调查一社区人们的幸福度.现从调查人群中随机抽取10名,以下茎叶图记录了他们的幸福度分数(以十位数字为茎,个位数字为叶);若幸福度不低于95分,则称该人的幸福度为“极幸福”.

(1)从这10人中随机选取3人,记![]() 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)以这10人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记![]() 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求![]() 的数学期望和方差.
的数学期望和方差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com