
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 由条件求得n=10,a0=1,在所给的等式中,令x=1+$\frac{1}{2}$,可得1+$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{n}}{{2}^{n}}$=0,即可求出$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{n}}{{2}^{n}}$的值.
解答 解:∵C${\;}_{2013}^{1006}$+C${\;}_{2013}^{1007}$=C${\;}_{n}^{\frac{n}{2}}$,
∴n=2014,
∵(2x-3)n=(2x-3)2014=[-1+2(x-1)]2014=a0+a1(x-1)1+…an(x-1)n,x∈R,n∈N,∴a0=1.
在[-1+2(x-1)]2014=a0+a1(x-1)1+…an(x-1)n中,令x=1+$\frac{1}{2}$,可得1+$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{n}}{{2}^{n}}$=0,
∴$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{n}}{{2}^{n}}$=-1,
故选:A.
点评 本题主要考查二项式定理的应用,是给变量赋值的问题,关键是根据要求的结果,选择合适的数值代入,属于中档题.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{π}{4}$,$\frac{π}{4}$) | B. | (0,$\frac{π}{4}$)∪($\frac{7π}{4}$,2π) | C. | (0,$\frac{π}{4}$)∪($\frac{5π}{4}$,$\frac{7π}{4}$) | D. | ($\frac{π}{4}$,$\frac{3π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
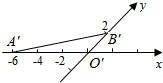 如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积是( )
如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积是( )| A. | 6 | B. | 3$\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com