
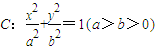 过点D(1,
过点D(1,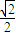 ),焦点为F1,F2,满足
),焦点为F1,F2,满足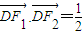 .
.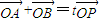 (其中O为坐标原点),求整数t的最大值.
(其中O为坐标原点),求整数t的最大值.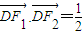 代入坐标后求出c的值,结合a2-b2=c2得到关于a,b的另一方程联立后可求解a,b的值,则椭圆方程可求;
代入坐标后求出c的值,结合a2-b2=c2得到关于a,b的另一方程联立后可求解a,b的值,则椭圆方程可求;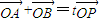 后得到P点的坐标,把P点坐标代入椭圆方程后得到t与k的关系,由k的范围确定t的范围.
后得到P点的坐标,把P点坐标代入椭圆方程后得到t与k的关系,由k的范围确定t的范围.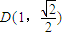 ,得
,得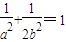 ,①
,①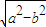 ,不妨设F1(-c,0),F2(c,0),则
,不妨设F1(-c,0),F2(c,0),则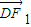 =(-c-1,-
=(-c-1,-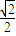 ),
),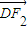 =(c-1,-
=(c-1,-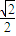 ),
),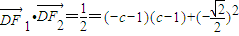 ,得c2=1,即a2-b2=1.②
,得c2=1,即a2-b2=1.②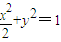 .
.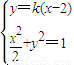 ,得(1+2k2)x2-8k2x+8k2-2=0.
,得(1+2k2)x2-8k2x+8k2-2=0.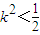 .
.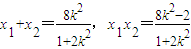 ,
,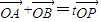 ,∴(x1+x2,y1+y2)=t(x,y).
,∴(x1+x2,y1+y2)=t(x,y).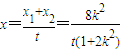 ,
,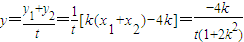
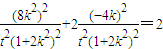 .
.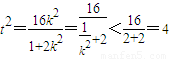 ,
,

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源:云南省建水一中2012届高三10月月考数学理科试题 题型:044
已知椭圆![]() 过点(0,1),且离心率为
过点(0,1),且离心率为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)A,B为椭圆C的左右顶点,直线l:x=2![]() 与x轴交于点D,点P是椭圆C上异于A,B的动点,直线AP,BP分别交直线l于E,F两点.证明:当点P在椭圆C上运动时,|DE|·|DF|恒为定值.
与x轴交于点D,点P是椭圆C上异于A,B的动点,直线AP,BP分别交直线l于E,F两点.证明:当点P在椭圆C上运动时,|DE|·|DF|恒为定值.
查看答案和解析>>
科目:高中数学 来源:陕西省延安中学2012届高三第七次模拟考试数学理科试题 题型:044
已知椭圆![]() 过点(0,1),且离心率为
过点(0,1),且离心率为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)A1,A2为椭圆C的左、右顶点,直线![]() 与x轴交于点D,点P是椭圆C上异于A1,A2的动点,直线A1P,A2P分别交直线l于E,F两点.证明:|DE|·|DF|恒为定值.
与x轴交于点D,点P是椭圆C上异于A1,A2的动点,直线A1P,A2P分别交直线l于E,F两点.证明:|DE|·|DF|恒为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆![]() 过点D(1,
过点D(1,![]() ),焦点为
),焦点为![]() ,满足
,满足![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若过点(2,0)的直线与椭圆C相交于两点A、B,P为椭圆上一点,且满足![]() (其中O为坐标原点),求整数t的最大值.
(其中O为坐标原点),求整数t的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com