
【题目】某市有![]() 三所高校,其学生会学习部有“干事”人数分别为
三所高校,其学生会学习部有“干事”人数分别为![]() ,现采用分层抽样的方法从这些“干事”中抽取
,现采用分层抽样的方法从这些“干事”中抽取![]() 名进行“大学生学习部活动现状”调查.
名进行“大学生学习部活动现状”调查.
(1)求应从![]() 这三所高校中分别抽取的“干事”人数;
这三所高校中分别抽取的“干事”人数;
(2)若从抽取的![]() 名干事中随机选两名干事,求选出的
名干事中随机选两名干事,求选出的![]() 名干事来自同一所高校的概率.
名干事来自同一所高校的概率.
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
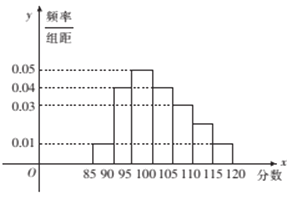
【题目】某校高二奥赛班![]() 名学生的物理测评成绩(满分120分)分布直方图如下,已知分数在100-110的学生数有21人.
名学生的物理测评成绩(满分120分)分布直方图如下,已知分数在100-110的学生数有21人.
(1)求总人数![]() 和分数在110-115分的人数
和分数在110-115分的人数![]() ;
;
(2)现准备从分数在110-115的![]() 名学生(女生占
名学生(女生占![]() )中任选3人,求其中恰好含有一名女生的概率;
)中任选3人,求其中恰好含有一名女生的概率;
(3)为了分析某个学生的学习状态,对其下一阶段的学生提供指导性建议,对他前7次考试的数学成绩![]() (满分150分),物理成绩
(满分150分),物理成绩![]() 进行分析,下面是该生7次考试的成绩.
进行分析,下面是该生7次考试的成绩.
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩![]() 与数学成绩
与数学成绩![]() 是线性相关的,若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
是线性相关的,若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
附:对于一组数据![]() ,
,![]() ……
……![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: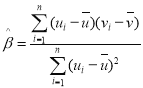 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() .
.

(1)在![]() 上确定一点
上确定一点![]() ,使得
,使得![]() 平面
平面![]() ,并求
,并求![]() 的值;
的值;
(2)在(1)条件下,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是圆
是圆![]() 上任意一点(
上任意一点(![]() 是圆心),点
是圆心),点![]() 与点
与点![]() 关于原点对称.线段
关于原点对称.线段![]() 的中垂线
的中垂线![]() 分别与
分别与![]() 交于
交于![]() 两点.
两点.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线经过![]() ,与抛物线
,与抛物线![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点.当以
两点.当以![]() 为直径的圆经过
为直径的圆经过![]() 时,求
时,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA![]() =4,点D是AB的中点
=4,点D是AB的中点

(1)求证:AC![]() BC
BC![]() ;
;
(2)求证:AC![]() //平面CDB
//平面CDB![]() ;
;
(3)求二面角B-DC-B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
将圆![]() 上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线
上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线![]() .
.
(1)写出曲线![]() 的参数方程;
的参数方程;
(2)以坐标原点为极点,![]() 轴正半轴为极轴坐标建立极坐标系,已知直线
轴正半轴为极轴坐标建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 分别为曲线
分别为曲线![]() 和直线
和直线![]() 上的一点,求
上的一点,求![]() 的最近距离.
的最近距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,二次函数
,二次函数![]() ,关于
,关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,其中
,其中![]() 为非零常数,设
为非零常数,设![]() .
.
(1)求![]() 的值;
的值;
(2)若存在一条与![]() 轴垂直的直线和函数
轴垂直的直线和函数![]() 的图象相切,且切点的横坐标
的图象相切,且切点的横坐标![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)当实数![]() 取何值时,函数
取何值时,函数![]() 存在极值?并求出相应的极值点.
存在极值?并求出相应的极值点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com