
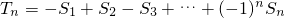 ,求满足不等式
,求满足不等式 的所有n的值;
的所有n的值;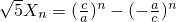 (n∈N+),证明:数列{
(n∈N+),证明:数列{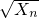 }中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.
}中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.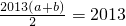 ,即a+b=2.
,即a+b=2.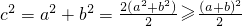 =
=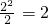 ,
, ;
;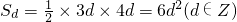 ,则
,则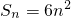 ,
, 得
得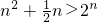 ,
,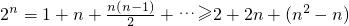 >
>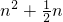 ,
,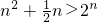 ,当n=1时,
,当n=1时,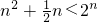 .
. 的所有n的值为2、3、4.
的所有n的值为2、3、4.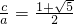 ,
,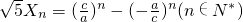 ,得
,得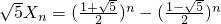 ,
,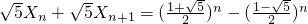
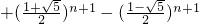
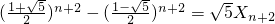 .
.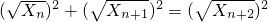 .
.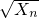 }中的任意连续三项为边长均可以构成直角三角形.
}中的任意连续三项为边长均可以构成直角三角形.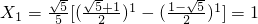 ,
,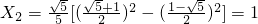 ,
,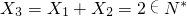 ,
,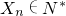 ,
,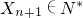 ?Xn+2∈N*,
?Xn+2∈N*, 的所有n的值;
的所有n的值; ,代入
,代入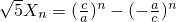 后整理,进一步得到
后整理,进一步得到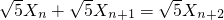 ,由此可证数列{
,由此可证数列{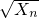 }中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.
}中的任意连续三项为边长均可以构成直角三角形,且Xn是正整数.

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
| 5 |
| c |
| a |
| a |
| c |
| Xn |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源:2013年广东省湛江市高考数学二模试卷(文科)(解析版) 题型:解答题
 相交于D、E两点,△CDE是以C(2,5)为直角顶点的等腰直角三角形,求该椭圆的方程.
相交于D、E两点,△CDE是以C(2,5)为直角顶点的等腰直角三角形,求该椭圆的方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com