
【题目】今有一组数据如下表:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 5 | 6 | 7 | 8 | 9 |
| 90 | 84 | 83 | m | 75 | 68 |
由最小二乘法求得点![]()
![]() 的回归直线方程是
的回归直线方程是![]() ,其中
,其中![]() .
.
(Ⅰ)求m的值,并求回归直线方程;
(Ⅱ)设![]() ,我们称
,我们称![]() 为点
为点![]() 的残差,记为
的残差,记为![]() .
.
从所给的点![]()
![]() 中任取两个,求其中有且只有一个点的残差绝对值不大于1的概率.
中任取两个,求其中有且只有一个点的残差绝对值不大于1的概率.
参考公式:  .
.
【答案】(1) m=80 , y= -4x+106. (2)![]()
【解析】试题分析:(1)将数据代入 ,可解得m=80,再求平均值,根据回归直线经过样本中心解得
,可解得m=80,再求平均值,根据回归直线经过样本中心解得![]() (2)根据枚举法列出总事件数为15个,从中确定其中有且只有一个点的残差绝对值不大于1的事件数为9,最后根据古典概型概率公式求概率
(2)根据枚举法列出总事件数为15个,从中确定其中有且只有一个点的残差绝对值不大于1的事件数为9,最后根据古典概型概率公式求概率
试题解析:解:(Ⅰ)![]() ,
,
由知![]() ,所以
,所以![]()
解得m=80
因回归直线经过样本中心![]() ,所以
,所以![]() ,
,
所以回归直线方程是y= -4x+106.
(Ⅱ)把点![]() 记为
记为![]() ,由(Ⅰ)得到回归直线方程可知
,由(Ⅰ)得到回归直线方程可知
![]() .
.
| 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 5 | 6 | 7 | 8 | 9 |
| 90 | 84 | 83 | 80 | 75 | 68 |
| 90 | 86 | 82 | 78 | 74 | 70 |
| 0 | 2 | 1 | 2 | 1 | 2 |
残差的绝对值不大于1的点共有3个:A1(4, 90),A3(6, 83),A5(8, 75).
从6个点中任取两个的基本事件:{A1,A2},{A1,A3},{A1,A4},{A1,A5},{A1,A6},
{A2,A3},{A2,A4},{A2,A5},{A2,A6},{A3,A4},{A3,A5},{A3,A6},{A4,A5},{A4,A6},{A5,A6} 共15个
两个点中有且只有一个点的残差绝对值不大于1的基本事件:
{A1,A2},{A1,A4},{A1,A6},{A2,A3},{A2,A5},{A3,A4},{A3,A6},{A4,A5},
{A5,A6} 共9个
所以在任取的两个点中,有且只有一个点的残差绝对值不大于1的槪率是
![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,M,N分别为
中,M,N分别为![]() 的中点.
的中点.
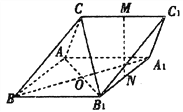
(1)证明:直线MN//平面CAB1;
(2)若四边形ABB1A1是菱形,且![]() ,
, ![]() ,求平面
,求平面![]() 和平面
和平面![]() 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() ,向量
,向量![]() ,
, ![]() ,经过点
,经过点![]() ,以
,以![]() 为方向向量的直线与经过点
为方向向量的直线与经过点![]() ,以
,以![]() 为方向向量的直线交于点
为方向向量的直线交于点![]() ,其中
,其中![]() .
.
(![]() )求点
)求点![]() 的轨迹方程,并指出轨迹
的轨迹方程,并指出轨迹![]() .
.
(![]() )若点
)若点![]() ,当
,当![]() 时,
时, ![]() 为轨迹
为轨迹![]() 上任意一点,求
上任意一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两神坐标系中的长度单位相同.已知曲线
轴的正半轴,两神坐标系中的长度单位相同.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)在曲线![]() 上求一点,使它到直线
上求一点,使它到直线![]() :
: 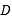 (
(![]() 为参数)的距离最短,写出
为参数)的距离最短,写出![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的对称中心为原点O,焦点在x轴上,离心率为![]() ,且点
,且点![]() 在该椭圆上。
在该椭圆上。
(I)求椭圆C的方程;
(II)过椭圆C的左焦点![]() 的直线l与椭圆C相交于
的直线l与椭圆C相交于![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,求圆心在原点O且与直线l相切的圆的方程。
,求圆心在原点O且与直线l相切的圆的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假定下述数据是甲、乙两个供货商的交货天数:
甲:10 9 10 10 11 11 9 11 10 10
乙:8 10 14 7 10 11 10 8 15 12
估计两个供货商的交货情况,并问哪个供货商交货时间短一些,哪个供货商交货时间较具一致性与可靠性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)五边形![]() 中,
中, ![]()
![]() ,将
,将![]() 沿
沿![]() 折到
折到![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() ,如图(2),点
,如图(2),点![]() 为线段
为线段![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与所成角的正切值为
与所成角的正切值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
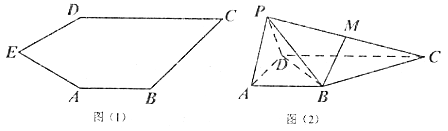
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com