

【题目】下面几种推理是类比推理的( )
A. 两条直线平行,同旁内角互补,如果![]() 和
和![]() 是两条平行直线的同旁内角,则
是两条平行直线的同旁内角,则![]()
B. 由平面三角形的性质,推测空间四边形的性质
C. 某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员.
D. 一切偶数都能被2整除,![]() 是偶数,所以
是偶数,所以![]() 能被2整除.
能被2整除.
科目:高中数学 来源: 题型:
【题目】某商场销售某种品牌的空调器,每周周初购进一定数量的空调器,商场每销售一台空调器可获利500元,若供大于求,则每台多余的空调器需交保管费100元;若供不应求,则可从其他商店调剂供应,此时每台空调器仅获利润200元。
(Ⅰ)若该商场周初购进20台空调器,求当周的利润(单位:元)关于当周需求量n(单位:台,![]() )的函数解析式
)的函数解析式![]() ;
;
(Ⅱ)该商场记录了去年夏天(共10周)空调器需求量n(单位:台),整理得下表:
周需求量n | 18 | 19 | 20 | 21 | 22 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10周记录的各需求量的频率作为各需求量发生的概率,若商场周初购进20台空调器,X表示当周的利润(单位:元),求X的分布列及数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(t,1)为函数y=ax2+bx+4(a,b为常数,且a≠0)与y=x图象的交点.
(1)求t;
(2)若函数y=ax2+bx+4的图象与x轴只有一个交点,求a,b;
(3)若1≤a≤2,设当![]() ≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n的最小值.
≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业2017年的纯利润为500万元,因设备老化等原因,企业的生产能力逐年下降,若不能进行技术改造,预测从2018年起每年比上一年纯利润减少20万元,2018年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第![]() 年(以2018年为第一年)的利润为
年(以2018年为第一年)的利润为![]() 万元(
万元(![]() 为正整数).
为正整数).
(1)设从今年起的前![]() 年,若该企业不进行技术改造的累计纯利润为
年,若该企业不进行技术改造的累计纯利润为![]() 万元,进行技术改造后的累计纯利润为
万元,进行技术改造后的累计纯利润为![]() 万元(须扣除技术改造资金),求
万元(须扣除技术改造资金),求![]() ,
,![]() 的表达式;
的表达式;
(2)依上述预测,从2018年起该企业至少经过多少年,进行技术改造后的累计利润超过不进行技术改造的累计纯利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() (
(![]() 为常数).
为常数).
(1)若函数![]() 与函数
与函数![]() 在
在![]() 处有相同的切线,求实数
处有相同的切线,求实数![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,证明:
,证明: ![]() ;
;
(3)若对任意![]() ,不等式恒
,不等式恒![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面是某市环保局连续30天对空气质量指数的监测数据:
61 76 70 56 81 91 55 91 75 81
88 67 101 103 57 91 77 86 81 83
82 82 64 79 86 85 75 71 49 45
(1)完成下面的频率分布表;
(2)完成下面的频率分布直方图,并写出频率分布直方图中![]() 的值;
的值;
(3)在本月空气质量指数大于等于91的这些天中随机选取两天,求这两天中至少有一天空气质量指数在区间![]() 内的概率.
内的概率.
分组 | 频数 | 频率 |
[41,51) | 2 |
|
[51,61) | 3 |
|
[61,71) | 4 |
|
[71,81) | 6 |
|
[81,91) | ||
[91,101) | 3 | |
[101,111) |
|
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(x0,y0)(x0≠![]() )在椭圆C:
)在椭圆C:![]() (a>b>0)上,若点M为椭圆C的右顶点,且PO⊥PM (O为坐标原点),则椭圆C的离心率e的取值范围是
(a>b>0)上,若点M为椭圆C的右顶点,且PO⊥PM (O为坐标原点),则椭圆C的离心率e的取值范围是
A. (0,![]() ) B. (0,1) C. (
) B. (0,1) C. (![]() ,1) D. (0,
,1) D. (0,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知直线
中,已知直线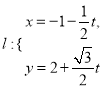 (
(![]() 为参数),曲线
为参数),曲线![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立坐标系.
轴的正半轴为极轴建立坐标系.
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的极坐标方程;
的极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了![]() 至
至![]() 月份每月
月份每月![]() 号的昼夜温差情况与因患感冒而就诊的人数,得到如下数据资料:
号的昼夜温差情况与因患感冒而就诊的人数,得到如下数据资料:
日期 |
|
|
|
|
|
|
昼夜温差 |
|
|
|
|
|
|
就诊人数 |
|
|
|
|
|
|
该兴趣小组确定的研究方案是:先从这![]() 组(每个有序数对
组(每个有序数对![]() 叫作一组)数据中随机选取
叫作一组)数据中随机选取![]() 组作为检验数据,用剩下的
组作为检验数据,用剩下的![]() 组数据求线性回归方程.
组数据求线性回归方程.
(Ⅰ)求选取的![]() 组数据恰好来自相邻两个月的概率;
组数据恰好来自相邻两个月的概率;
(Ⅱ)若选取的是![]() 月和
月和![]() 月的两组数据,请根据
月的两组数据,请根据![]() 至
至![]() 月份的数据,求出
月份的数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅲ)若由线性回归方程得到的估计数据与所选取的检验数据的误差均不超过![]() 人,则认为得到的线性回归方程是理想的,试问(Ⅱ)中所得到的线性回归方程是否是理想的?
人,则认为得到的线性回归方程是理想的,试问(Ⅱ)中所得到的线性回归方程是否是理想的?
参考公式: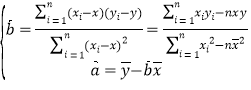 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com